Matrices: A beginner's guide

Matrices as Operations on Quantum States

The states of a quantum system can be written as

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{\psi}\right\rangle = \alpha_0\left\vert{0}\right\rangle + \alpha_1\left\vert{1}\right\rangle,}	(m.1)

where $\alpha _{0}\,\!$ and $\alpha _{1}\,\!$ are complex numbers. These states are used to represent quantum systems that can be used to store information. Because $|\alpha _{0}|^{2}\,\!$ and $|\alpha _{1}|^{2}\,\!$ are probabilities and must add up to one,

	$|\alpha _{0}|^{2}+|\alpha _{1}|^{2}=1.\,\!$	(m.2)

This means that this vector is normalized, i.e. its magnitude (or length) is one. (Appendix B contains a basic introduction to complex numbers.) The basis vectors for such a space are the two vectors $\left\vert {0}\right\rangle$ and $\left\vert {1}\right\rangle$ which are called computational basis states. These two basis states are represented by

	$\left\vert {0}\right\rangle =\left({\begin{array}{c}1\\0\end{array}}\right),\;\;\left\vert {1}\right\rangle =\left({\begin{array}{c}0\\1\end{array}}\right).$	(m.3)

Thus, the qubit state can be rewritten as

	$\left\vert {\psi }\right\rangle =\left({\begin{array}{c}\alpha _{0}\\\alpha _{1}\end{array}}\right).$	(m.4)

A very common operation in computing is to change a $0$ to a $1$ and a $1$ to a $0$. The operation that does this is denoted a $X$. This operator does both. It changes $0$ a $1$ and $1$ to $0$. So we write,

	$X\left|0\right\rangle =\left|1\right\rangle ,{\mbox{ and }}X\left|1\right\rangle =\left|0\right\rangle .\,\!$	(m.1)

Notice that this means that acting with $X$ again means that you get back the original state. Matrices, which are arrays of numbers, are the mathematical incarnation of these operations. It turns out that matrices are the way to represent almost all of operations in quantum computing and this will be shown in this section.

Let us list some important matrices that will be used as examples below:

	$X=\left({\begin{array}{cc}0&1\\1&0\end{array}}\right),\,\!$	(m.1)

	$Z=\left({\begin{array}{cc}1&0\\0&-1\end{array}}\right),\,\!$	(m.2)

	$Y=\left({\begin{array}{cc}0&-i\\i&0\end{array}}\right),\,\!$	(m.3)

	$H=\left({\begin{array}{cc}1/{\sqrt {2}}&1/{\sqrt {2}}\\1/{\sqrt {2}}&-1/{\sqrt {2}}\end{array}}\right).\,\!$	(m.3)

These all have the general form

	$M=\left({\begin{array}{cc}a&b\\c&d\end{array}}\right),\,\!$	(m.4)

where the numbers $a,b,c,d$ can be complex numbers.

Matrices

Basic Definition and Representations

A matrix is an array of numbers of the following form with columns, col. 1, col. 2, etc., and rows, row 1, row 2, etc. The entries for the matrix are labeled by the row and column. So the entry of a matrix $A$ will be $a_{ij}$ where $i$ is the row and $j$ is the column where the number $a_{ij}$ is found. This is how it looks:

$A={\begin{array}{c}{\scriptstyle {row\;1}}\\{\scriptstyle {row\;2}}\\\vdots \\{\scriptstyle {row\;m}}\end{array}}{\overset {{\scriptstyle {col.\;1}}\;\;\;{\scriptstyle {col.\;2}}\;\;\;\;{\displaystyle {\cdots }}\;\;\;\;\;{\scriptstyle {col.\;n}}}{\left({\begin{array}{cccc}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{array}}\right)}}.\,\!$

Notice that we represent the whole matrix with a capital letter $A$. The matrix $A$ has $m$ rows and $n$ columns, so we say that $A$ is an $m\times n$ matrix. We could also represent it using all of the entries, this array of numbers seen in the equation above. Another way to represent it is to write it as $(a_{ij})$. By this we mean that it is the array of numbers in the parentheses.

Examples

The matrix above,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X = \left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \,\!}	(m.1)

is a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 2} matrix.

The matrix

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = \left(\begin{array}{ccc} 3 & 2 & 5 \\ 1 & 0 & 4\end{array}\right), \,\!}	(m.1)

is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 3} and

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = \left(\begin{array}{cc} 2 & 5 \\ 1 & 4 \\ 7 & 0 \\ 8 & 3\end{array}\right), \,\!}	(m.1)

is a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\times 2} matrix.

Matrix Addition

Matrix addition is performed by adding each element of one matrix with the corresponding element in another matrix. Let our two matrices be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} as above, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} . To represent these in an array,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array}\right), \;\;\;\; B = \left(\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \end{array}\right). \,\!}

The the sum, which we could call Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C= A+B} is given by

$A+B=\left({\begin{array}{cccc}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{array}}\right)+\left({\begin{array}{cccc}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\end{array}}\right)=\left({\begin{array}{cccc}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\end{array}}\right).\,\!$

In other words, the sum gives $c_{11}=a_{11}+b_{11}\,\!$, etc. We add them component by component like we do vectors.

Change the font color or type in order to highlight the entries that are being added.

Multiplying a Matrix by a Number

When multiplying a matrix by a number, each element of the matrix gets multiplied by that number. Seem familiar? This is what was done for vectors.

Let $k$ be some number. Then

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle kA = k\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array}\right) = \left(\begin{array}{cccc} ka_{11} & ka_{12} & \cdots & ka_{1n} \\ ka_{21} & ka_{22} & \cdots & ka_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ ka_{m1} & ka_{m2} & \cdots & ka_{mn} \end{array}\right) \,\!}

Multiplying two Matrices

The the product, which we could call Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C= AB} is given by

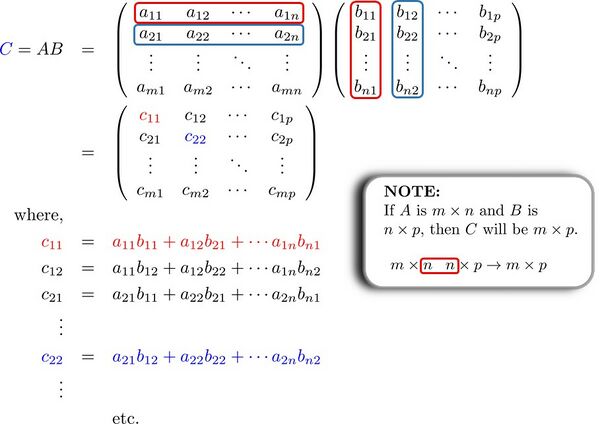
Examples

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \left(\begin{array}{cc} 2 & 3 \\ 5 & 6 \end{array}\right), \mbox{ and } B = \left(\begin{array}{cc} 1 & 4 \\ 7 & 2 \end{array}\right) \,\!}	(m.1)

Then

	$AB=\left({\begin{array}{cc}2&3\\5&6\end{array}}\right)\left({\begin{array}{cc}1&4\\7&2\end{array}}\right)=\left({\begin{array}{cc}2\cdot 1+3\cdot 7&2\cdot 4+3\cdot 2\\5\cdot 1+6\cdot 7&5\cdot 4+6\cdot 2\end{array}}\right)=\left({\begin{array}{cc}23&14\\47&32\end{array}}\right),\,\!$	(m.1)

Let us multiply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} from above,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X Z = \left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) = \left(\begin{array}{cc} 0\cdot 1 + 1\cdot 0 & 0\cdot 0 + 1\cdot (-1) \\ 1\cdot 1 + 0\cdot 0 & 1\cdot 0 + 0\cdot (-1) \end{array}\right) = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right), \,\!}	(m.1)

It is helpful to notice that this is $-iY$; that is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XZ = -i Y} .

Notation

There are many aspects of linear algebra that are quite useful in quantum mechanics. We will briefly discuss several of these aspects here. First, some definitions and properties are provided that will be useful. Some familiarity with matrices will be assumed, although many basic definitions are also included.

Let us denote some Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\times n\,\!} matrix by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} . The set of all $m\times n\,\!$ matrices with real entries is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(m\times n,\mathbb{R})\,\!} . Such matrices are said to be real since they have all real entries. Similarly, the set of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\times n\,\!} complex matrices is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(m\times n,\mathbb{C})\,\!} . For the set of square $n\times n\,\!$ complex matrices, we simply write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(n,\mathbb{C})\,\!} .

We will also refer to the set of matrix elements, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{ij}\,\!} , where the first index (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\,\!} in this case) labels the row and the second $(j)\,\!$ labels the column. Thus the element Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{23}\,\!} is the element in the second row and third column. A comma is inserted if there is some ambiguity. For example, in a large matrix the element in the 2nd row and 12th column is written as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{2,12}\,\!} to distinguish between the 21st row and 2nd column.

The Identity Matrix

An identity matrix has the property that when it is multiplied by any matrix, that matrix is unchanged. That is, for any matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} ,

$\mathbb {I} A=A\mathbb {I} =A.\,\!$

Such an identity matrix always has ones along the diagonal and zeroes everywhere else. For example, the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \times 3\,\!} identity matrix is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I} = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right). \,\!}

It is straight-forward to verify that any Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \times 3\,\!} matrix is not changed when multiplied by the identity matrix.

Complex Conjugate

The complex conjugate of a matrix is the matrix with each element replaced by its complex conjugate. In other words, to take the complex conjugate of a matrix, one takes the complex conjugate of each entry in the matrix. We denote the complex conjugate with a star, like this: $A^{*}\,\!$. For example,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} A^* &=& \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right)^* \\ &=& \left(\begin{array}{ccc} a_{11}^* & a_{12}^* & a_{13}^* \\ a_{21}^* & a_{22}^* & a_{23}^* \\ a_{31}^* & a_{32}^* & a_{33}^* \end{array}\right). \end{align} \,\!}	(C.2)

(Notice that the notation for a matrix is a capital letter, whereas the entries are represented by lower case letters.)

Transpose

The transpose of a matrix is the same set of elements, but now the first row becomes the first column, the second row becomes the second column, and so on. Thus the rows and columns are interchanged. For example, for a square Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3\,\!} matrix, the transpose is given by

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} A^T &=& \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right)^T \\ &=& \left(\begin{array}{ccc} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{array}\right). \end{align} \,\!}	(C.3)

Hermitian Conjugate

The complex conjugate and transpose of a matrix is called the Hermitian conjugate, or simply the dagger of a matrix. It is called the dagger because the symbol used to denote it, ($\dagger \,\!$):

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A^T)^* = (A^*)^T \equiv A^\dagger. \,\!}	(C.4)

For our Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3\,\!} example,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^\dagger = \left(\begin{array}{ccc} a_{11}^* & a_{21}^* & a_{31}^* \\ a_{12}^* & a_{22}^* & a_{32}^* \\ a_{13}^* & a_{23}^* & a_{33}^* \end{array}\right). \,\!}

If a matrix is its own Hermitian conjugate, i.e. $A^{\dagger }=A\,\!$, then we call it a Hermitian matrix. (Clearly this is only possible for square matrices.) Hermitian matrices are very important in quantum mechanics since their eigenvalues are real. (See Sec.(Eigenvalues and Eigenvectors).)

Index Notation

Very often we write the product of two matrices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\,\!} simply as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB\,\!} and let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=AB\,\!} . However, it is also quite useful to write this in component form. In this case, if these are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\times n\,\!} matrices, the component form will be

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ik} = \sum_{j=1}^n a_{ij}b_{jk}. \,\!}

This says that the element in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{\mbox{th}}\,\!} row and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^{\mbox{th}}\,\!} column of the matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\,\!} is the sum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1}^n a_{ij}b_{jk}\,\!} . The transpose of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\,\!} has elements

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ki} = \sum_{j=1}^n a_{kj}b_{ji}. \,\!}

Now if we were to transpose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\,\!} as well, this would read

$c_{ki}=\sum _{j=1}^{n}(a_{jk})^{T}(b_{ij})^{T}=\sum _{j=1}^{n}b_{ij}^{T}a_{jk}^{T}.\,\!$

This gives us a way of seeing the general rule that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^T = B^TA^T. \,\!}

It follows that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^\dagger = B^\dagger A^\dagger. \,\!}

The Trace

The trace of a matrix is the sum of the diagonal elements and is denoted Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{Tr}\,\!} . So for example, the trace of an $n\times n\,\!$ matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{Tr}(A) = \sum_{i=1}^n a_{ii} \,\!} .

Some useful properties of the trace are the following:

1. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{Tr}(AB) = \mbox{Tr}(BA)\,\!}
2. ${\mbox{Tr}}(A+B)={\mbox{Tr}}(A)+{\mbox{Tr}}(B)\,\!$.

Using the first of these results,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{Tr}(UAU^{-1}) = \mbox{Tr}(U^{-1}UA) = \mbox{Tr}(A). \,\!}

This relation is used so often that we state it here explicitly.

The Determinant

For a square matrix, the determinant is quite a useful thing. For example, an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\times n\,\!} matrix is invertible if and only if its determinant is not zero. So let us define the determinant and give some properties and examples.

The determinant of a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 2\,\!} matrix,

	$N=\left({\begin{array}{cc}a&b\\c&d\end{array}}\right),\,\!$	(C.5)

is given by

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(N) = ad-bc. \,\!}	(C.6)

Higher-order determinants can be written in terms of smaller ones in a recursive way. For example, let

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = \left(\begin{array}{ccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33}\end{array}\right). \,\!}

Then

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(M) = m_{11}\det\left(\begin{array}{cc} m_{22} & m_{23} \\ m_{32} & m_{33} \end{array}\right) - m_{12}\det\left(\begin{array}{cc} m_{21} & m_{23} \\ m_{31} & m_{33} \end{array}\right) +m_{13}\det\left(\begin{array}{cc} m_{21} & m_{22} \\ m_{31} & m_{32} \end{array}\right). \,\!}

The determinant of a matrix $A\,\!$ can be also be written in terms of its components as

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A) = \sum_{i,j,k,l,...} \epsilon_{ijkl...} a_{1i}a_{2j}a_{3k}a_{4l} ..., \,\!}	(C.7)

where the symbol

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{ijkl...} = \begin{cases} +1, \; \mbox{if } \; ijkl... = 1234... (\mbox{in order, or any even number of permutations}),\\ -1, \; \mbox{if } \; ijkl... = 2134... (\mbox{or any odd number of permutations}),\\ \;\;\; 0, \; \mbox{otherwise}, \; (\mbox{meaning any index is repeated}). \end{cases} \,\!}	(C.8)

Let us consider the example of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3\,\!} matrix $A\,\!$ given above. The determinant can be calculated by

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A) = \sum_{i,j,k} \epsilon_{ijk} a_{1i}a_{2j}a_{3k}, \,\!}

where, explicitly,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{ijk} = \begin{cases} +1, \;\mbox{if }\; ijk= 123,231,\; \mbox{or}\; 312, (\mbox{These are even permutations of }123),\\ -1, \;\mbox{if }\; ijk = 213,132,\;\mbox{or}\;321(\mbox{These are odd permuations of }123),\\ \;\;\; 0, \; \mbox{otherwise}, \; (\mbox{meaning any index is repeated}), \end{cases} \,\!}	(C.9)

so that

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \det(A) &=& \epsilon_{123}a_{11}a_{22}a_{33} +\epsilon_{132}a_{11}a_{23}a_{32} +\epsilon_{231}a_{12}a_{23}a_{31} \\ &&+\epsilon_{213}a_{12}a_{21}a_{33} +\epsilon_{312}a_{13}a_{21}a_{32} +\epsilon_{321}a_{13}a_{22}a_{31}. \end{align} \,\!}	(C.10)

Now given the values of $\epsilon _{ijk}\,\!$ in Eq. C.9, this is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A) = a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} + a_{12}a_{23}a_{31} - a_{12}a_{21}a_{33} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}. \,\!}

The determinant has several properties that are useful to know. A few are listed here:

1. The determinant of the transpose of a matrix is the same as the determinant of the matrix itself: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A) = \det(A^T).\,\!}
2. The determinant of a product is the product of determinants: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(AB) = \det(A)\det(B).\,\!}

From this last property, another specific property can be derived. If we take the determinant of the product of a matrix and its inverse, we find

$\det(UU^{-1})=\det(U)\det(U^{-1})=\det(\mathbb {I} )=1,\,\!$

since the determinant of the identity is one. This implies that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(U^{-1}) = \frac{1}{\det(U)}. \,\!}

The Inverse of a Matrix

The inverse of an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\times n\,\!} square matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\,\!} is another $n\times n\,\!$ square matrix, denoted Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}\,\!} , such that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AA^{-1} = A^{-1}A = \mathbb{I}, \,\!}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} is the identity matrix consisting of zeroes everywhere except the diagonal, which has ones. For example, the $3\times 3\,\!$ identity matrix is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}_3 = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right). \,\!}

It is important to note that a matrix is invertible if and only if its determinant is nonzero. Thus one only needs to calculate the determinant to see if a matrix has an inverse or not.

Hermitian Matrices

Hermitian matrices are important for a variety of reasons; primarily, it is because their eigenvalues are real. Thus Hermitian matrices are used to represent density operators and density matrices, as well as Hamiltonians. The density operator is a positive semi-definite Hermitian matrix (it has no negative eigenvalues) that has its trace equal to one. In any case, it is often desirable to represent Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\times N\,\!} Hermitian matrices using a real linear combination of a complete set of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\times N\,\!} Hermitian matrices. A set of $N\times N\,\!$ Hermitian matrices is complete if any Hermitian matrix can be represented in terms of the set. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\lambda_i\}\,\!} be a complete set. Then any Hermitian matrix can be represented by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_i a_i \lambda_i\,\!} . The set can always be taken to be a set of traceless Hermitian matrices and the identity matrix. This is convenient for the density matrix (its trace is one) because the identity part of an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\times N\,\!} Hermitian matrix is $(1/N)\mathbb {I} \,\!$ if we take all others in the set to be traceless. For the Hamiltonian, the set consists of a traceless part and an identity part where identity part just gives an overall phase which can often be neglected.

One example of such a set which is extremely useful is the set of Pauli matrices. These are discussed in detail in Chapter 2 and in particular in Section 2.4.

Unitary Matrices

A unitary matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\,\!} is one whose inverse is also its Hermitian conjugate, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^\dagger = U^{-1}\,\!} , so that

$U^{\dagger }U=UU^{\dagger }=\mathbb {I} .\,\!$

If the unitary matrix also has determinant one, it is said to be a special unitary matrix. The set of $n\times n\,\!$ unitary matrices is denoted $U(n)\,\!$ and the set of special unitary matrices is denoted $SU(n)\,\!$.

Unitary matrices are particularly important in quantum mechanics because they describe the evolution of quantum states. They have this ability due to the fact that the rows and columns of unitary matrices (viewed as vectors) are orthonormal. (This is made clear in an example below.) This means that when they act on a basis vector of the form

	$\left\vert j\right\rangle =\left({\begin{array}{c}0\\0\\\vdots \\1\\\vdots \\0\end{array}}\right),\,\!$	(C.11)

with a single 1, in say the $j$th spot, and zeroes everywhere else, the result is a normalized complex vector. Acting on a set of orthonormal vectors of the form given in Eq.(C.11) will produce another orthonormal set.

Let us consider the example of a $2\times 2\,\!$ unitary matrix,

	$U=\left({\begin{array}{cc}a&b\\c&d\end{array}}\right).\,\!$	(C.12)

The inverse of this matrix is the Hermitian conjugate,

	$U^{-1}=U^{\dagger }=\left({\begin{array}{cc}a^{*}&c^{*}\\b^{*}&d^{*}\end{array}}\right),\,\!$	(C.13)

provided that the matrix $U\,\!$ satisfies the constraints

	${\begin{aligned}|a|^{2}+|b|^{2}=1,\;&\;ac^{*}+bd^{*}=0\\ca^{*}+db^{*}=0,\;&\;|c|^{2}+|d|^{2}=1,\end{aligned}}\,\!$	(C.14)

and

	${\begin{aligned}|a|^{2}+|c|^{2}=1,\;&\;ba^{*}+dc^{*}=0\\b^{*}a+d^{*}c=0,\;&\;|b|^{2}+|d|^{2}=1.\end{aligned}}\,\!$	(C.15)

Looking at each row as a vector, the constraints in Eq.(C.14) are the orthonormality conditions for the vectors forming the rows. Similarly, the constraints in Eq.(C.15) are the orthonormality conditions for the vectors forming the columns.

Inner and Outer Products

It is very helpful to note that a column vector with $n\times 1\,\!$ matrix. A row vector is a $1\times n\,\!$ matrix.

Now that we have a definition for the Hermitian conjugate, consider the case for a $n\times 1\,\!$ matrix, i.e. a vector. In Dirac notation, this is

$\left\vert \psi \right\rangle =\left({\begin{array}{c}\alpha \\\beta \end{array}}\right).\,\!$

The Hermitian conjugate comes up so often that we use the following notation for vectors:

$\left\langle \psi \right\vert =(\left\vert \psi \right\rangle )^{\dagger }=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{\dagger }=\left(\alpha ^{*},\;\beta ^{*}\right).\,\!$

This is a row vector and in Dirac notation is denoted by the symbol $\left\langle \cdot \right\vert \!$, which is called a bra. Let us consider a second complex vector,

$\left\vert \phi \right\rangle =\left({\begin{array}{c}\gamma \\\delta \end{array}}\right).\,\!$

The inner product between $\left\vert \psi \right\rangle \,\!$ and $\left\vert \phi \right\rangle \,\!$ is computed as follows:

	${\begin{aligned}\left\langle \phi \mid \psi \right\rangle &\equiv (\left\vert \phi \right\rangle )^{\dagger }\left\vert \psi \right\rangle \\&=(\gamma ^{*},\delta ^{*})\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\gamma ^{*}\alpha +\delta ^{*}\beta .\end{aligned}}$	(C.16)

The vector $\left|\cdot \right\rangle \!$ is called a ket. When you put a bra together with a ket, you get a bracket. This is the origin of the terms.

The outer product between these same two vectors is

${\begin{aligned}(\left\vert \phi \right\rangle )(\left\vert \psi \right\rangle )^{\dagger }&=\left\vert \phi \right\rangle \left\langle \psi \right\vert \\&=\left({\begin{array}{c}\gamma \\\delta \end{array}}\right)\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{\dagger }\\&=\left({\begin{array}{c}\gamma \\\delta \end{array}}\right)\left({\begin{array}{cc}\alpha ^{*}&\beta ^{*}\end{array}}\right)\\&=\left({\begin{array}{cc}\gamma \alpha ^{*}&\gamma \beta ^{*}\\\delta \alpha ^{*}&\delta \beta ^{*}\end{array}}\right)\end{aligned}}\;\!$

This type of product is also called a Kronecker product or a tensor product. Vectors and matrices can be considered special cases of the more general class of tensors. A tensor can have any number of indices indicating rows, columns, and depth, for the case of a three index tensor.

Unitary Matrices

A unitary matrix $U\,\!$ is one whose inverse is also its Hermitian conjugate, $U^{\dagger }=U^{-1}\,\!$, so that

$U^{\dagger }U=UU^{\dagger }=\mathbb {I} .\,\!$

If the unitary matrix also has determinant one, it is said to be a special unitary matrix. The set of $n\times n\,\!$ unitary matrices is denoted $U(n)\,\!$ and the set of special unitary matrices is denoted $SU(n)\,\!$.

Unitary matrices are particularly important in quantum mechanics because they describe the evolution of quantum states. They have this ability due to the fact that the rows and columns of unitary matrices (viewed as vectors) are orthonormal. (This is made clear in an example below.) This means that when they act on a basis vector of the form

	$\left\vert j\right\rangle =\left({\begin{array}{c}0\\0\\\vdots \\1\\\vdots \\0\end{array}}\right),\,\!$	(C.11)

with a single 1, in say the $j$th spot, and zeroes everywhere else, the result is a normalized complex vector. Acting on a set of orthonormal vectors of the form given in Eq.(C.11) will produce another orthonormal set.

Let us consider the example of a $2\times 2\,\!$ unitary matrix,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = \left(\begin{array}{cc} a & b \\ c & d \end{array}\right). \,\!}	(C.12)

The inverse of this matrix is the Hermitian conjugate,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U ^{-1} = U^\dagger = \left(\begin{array}{cc} a^* & c^* \\ b^* & d^* \end{array}\right), \,\!}	(C.13)

provided that the matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\,\!} satisfies the constraints

	${\begin{aligned}|a|^{2}+|b|^{2}=1,\;&\;ac^{*}+bd^{*}=0\\ca^{*}+db^{*}=0,\;&\;|c|^{2}+|d|^{2}=1,\end{aligned}}\,\!$	(C.14)

and

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |a|^2 + |c|^2 = 1, \; & \; ba^*+dc^* =0 \\ b^*a+d^*c=0, \; & \; |b|^2 + |d|^2 =1. \end{align}\,\!}	(C.15)

Looking at each row as a vector, the constraints in Eq.(C.14) are the orthonormality conditions for the vectors forming the rows. Similarly, the constraints in Eq.(C.15) are the orthonormality conditions for the vectors forming the columns.

Unitary matrices are very important because the preserve the magnitude of a complex vector. In other words, if if the magnitude of a vector is one, for example Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\big{|\}} |\psi\right\rangle {\big{||}} = 1\,\!} , then