Appendix B - Complex Numbers

Complex numbers arise naturally from an attempt to solve the equation

$a^{2}+1=0.\,\!$

It's easy enough to write such an equation down, but how would you solve it? The answer is

$a=\pm {\sqrt {-1}}=\pm i.\,\!$

We let the symbol $i\,\!$ represent ${\sqrt {-1}}\,\!$, so that $i^{2}=-1\,\!$. Then any number of the form

$z=x+iy,\,\!$

where $x\,\!$ and $y\,\!$ are real is called a complex number. Let's take some other complex number to be $\eta =c+id\,\!$ where $c\,\!$ and $d\,\!$ are real. Then the two complex numbers are equal,

$\eta =z.\,\!$

This means that

$x+iy=c+id,\,\!$

is true if and only if

$x=c,\;\;{\mbox{ and }}\;\;y=d.\,\!$

We refer to $x\,\!$ as the real part of the complex number $z\,\!$ and $y\,\!$ as the imaginary part. Sometimes these are written as Re($z\,\!$) and Im($z\,\!$) respectively.

We may restate the equivalence condition as $z=\eta \,\!$ if and only if the real part of $z\,\!$ is equal to the real part of $\eta \,\!$ and the imaginary part of $z\,\!$ is equal to the imaginary part of $\eta \,\!$.

To add two complex numbers, add the real parts and the imaginary parts separately:

$z+\eta =(x+iy)+(c+id)=(x+c)+i(y+d).\,\!$

Complex numbers are multiplied like any other binomial expression:

$z\eta =(x+iy)(c+id)=xc-yd+i(yc+xd),\,\!$

where we have used $i^{2}=-1\,\!$.

The complex conjugate of the complex number $z\,\!$ is denoted $z^{*}\,\!$ and is given by

$z^{*}=x-iy.\,\!$

One reason for defining this is that a number times its own complex conjugate is real,

$zz^{*}=(x+iy)(x-iy)=x^{2}+y^{2}+i(xy-yx)=x^{2}+y^{2}.\,\!$

Note that the complex conjugate of the complex conjugate is the original complex number, and

$z^{*}z=(x-iy)(x+iy)=x^{2}+y^{2}+i(yx-xy)=x^{2}+y^{2}=zz^{*}.\,\!$

We also call this the modulus squared . The modulus is

$|z|={\sqrt {(z^{*}z)}}={\sqrt {x^{2}+y^{2}}}.\,\!$

Note that the complex conjugate of a product is the product of the complex conjugates:

$(z\eta )^{*}=z^{*}\eta ^{*}.\,\!$

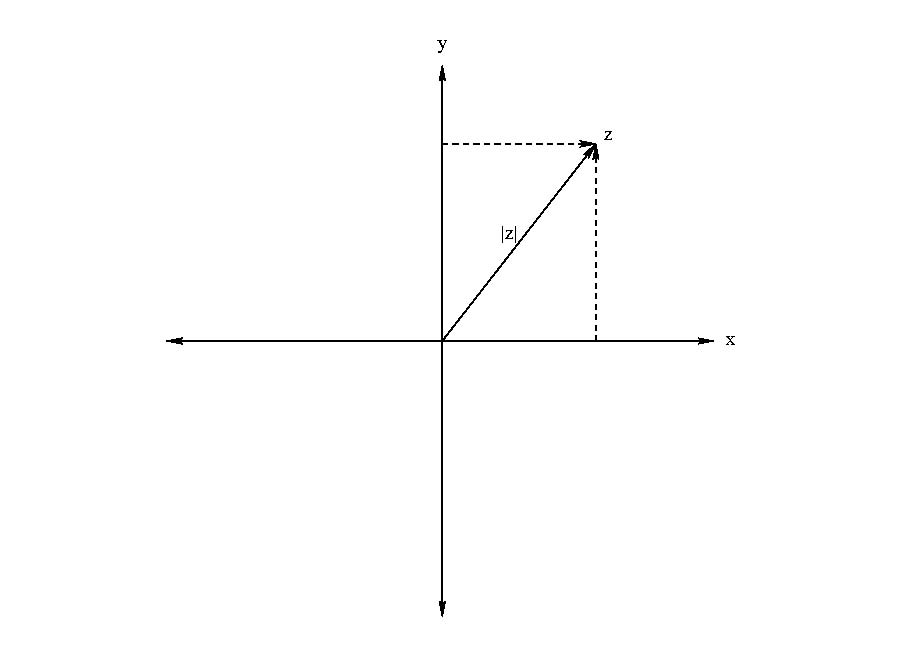
It is often useful to look at a graph for a complex number, consisting of an x-axis for the real part and a y-axis for the complex part. This is shown in Fig. B.1. In this way, we can think of $z\,\!$ as a two-dimensional vector with the magnitude (length) being equivalent to the modulus of the complex number, $|z|={\sqrt {x^{2}+y^{2}}}\,\!$.

Figure B.1: A complex number in Cartesian coordinates.

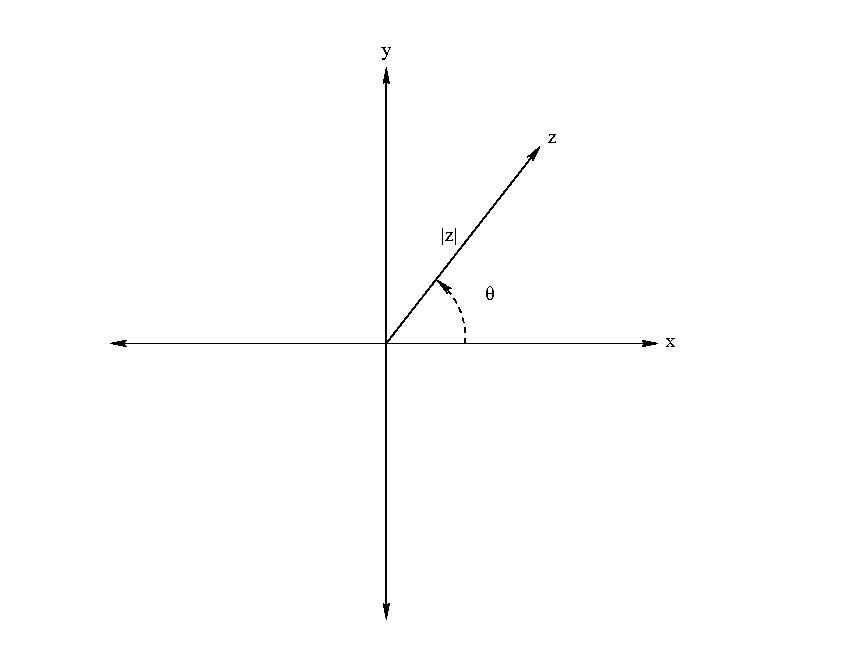
Another useful way to represent this is with polar coordinates. We can do this by writing

$z=|z|(\cos \theta +i\sin \theta ).\,\!$

Clearly if we wanted to rewrite this in terms of $x\,\!$ and $y\,\!$, we find that $x=|z|\cos \theta \,\!$ and $y=|z|\sin \theta \,\!$.

It turns out that

$e^{i\theta }=\cos \theta +i\sin \theta ,\,\!$

so we could also write

$z=|z|e^{i\theta }.\,\!$

This is really just a short-hand notation for us and most of the time, when we calculate something, we will use the $\sin \theta ,\cos \theta \,\!$ functions. But is often the case that people will write this as

$z=re^{i\theta },\,\!$

where $r={\sqrt {x^{2}+y^{2}}}\,\!$ as is usual for polar coordinates. So everything is just like polar coordinates with the exception of the inclusion of the factor $i\,\!$. (See Fig. B.2.)

Figure B.2: A polar coordinate representation of a complex number.

Exercises

• Ghost Directory - North America:
  • United States of America.
    • Florida.
    • New York.
      • Long Island
      • Manhattan
      • Cooney Island
    • New Jersey
    • Michigan
• Ghost Directory - Europe:
  • United Kingdom
    • Liverpool
    • Fulham
  • Ireland
  • Finland
  • Sweden

Other directories.

• Bangladesh
• India.

$z_{1}=5+2i\,\!$