Chapter 10 - Fault-Tolerant Quantum Computing

Introduction

As the name implies, fault-tolerant quantum computing means that quantum computations can be performed in spite of errors in the computation. To ensure that a computation is reliable, one must be able to prevent errors from accumulating. This could happen, for example, if a small error occurs on one qubit and propagates to many others before it is fixed. What are all the ways in which a error can occur and how can they be prevented from accumulating to produce erroneous results? In this chapter, these questions are addressed.

Requirements for Fault-Tolerance

As Preskill puts it in Lo, Popescu, and Spiller, one needs to "...sniff out all the ways in which a recovery failure could result from a single error, ..." Then, in a Proc. Roy. Soc. London article, he gives five laws for reliable quantum computing, as he reviews the results obtained for avoiding failure. Here, a slightly modified list is discussed. The list is

1. Be careful not to propagate errors,
2. Copy errors not data,
3. Carefully prepare ancilla,
4. Verify ancilla,
5. Verify the syndrome,
6. Take care with measurements.

All of these require some explanation. Let us take them in order.

1. Propagation of Errors

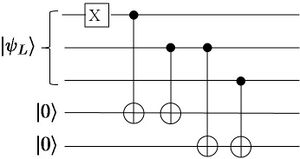
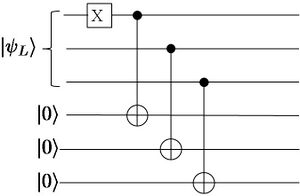
The general statements are that an error should not propagate within a code block and errors should not accumulate. For example, one should be careful when qubits are reused because error correction procedures can actually propagate errors. Consider the syndrome measurement in Figure 7.2. In that circuit, one of the ancillary qubits is used twice to check the parity of a pair of qubits in the bit-flip code. This, however, can propagate a single error in the ancilla to two qubits in the code block. However, this code can only detect and correct one error. Thus such an event would lead to failure.

Figure 7.3

Figure 7.3: Two different syndrome extraction circuits for the three-qubit quantum error correcting code. The figure on the left is not fault-tolerant. It is the same as Figure 7.2. The figure on the right is fault-tolerant. However, as explained in the text, it cannot be used.

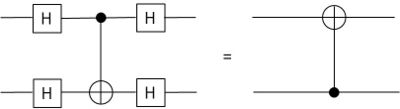
At first this may not seem likely. After all, the target bit is the one that is affected. However, as shown in Figure 7.4 errors can actually propagate from the target to the source, not just from the source to the target, in the CNOT operation.

Figure 7.4

Figure 7.4: The above circuit identity was used by Preskill to show that errors can propagate in not-so-obvious ways. In this particular case, an error can propagate from the source qubit as well as propagating to the target qubit in a CNOT gate.

The general rule is that an error of order

	${\begin{aligned}&=\\&=\end{aligned}}\,\!$	(7.?)

2. Copy Errors Not Data

The reason we cannot just use one ancilla for each qubit is that this gives information contained in the computation. If all ancilla are measured the superposition of $\alpha \,\!$ and $\beta \,\!$ will be destroyed.

Preparing the Ancilla

So what can we do? The answer is that we need to use a different recovery procedure. For example, we can modify our ancillary system.

Fault-Tolerant Quantum Computing for the Steane Code

$\,\!$