Chapter 10 - Fault-Tolerant Quantum Computing

Introduction

As the name implies, fault-tolerant quantum computing means that quantum computations can be performed in spite of errors in the computation. To ensure that a computation is reliable, one must be able to prevent errors from accumulating. This could happen, for example, if a small error occurs on one qubit and propagates to many others before it is fixed. What are all the ways in which a error can occur and how can they be prevented from accumulating to produce erroneous results? In this chapter, these questions are addressed.

Requirements for Fault-Tolerance

As Preskill puts it in Lo, Popescu, and Spiller, one needs to "...sniff out all the ways in which a recovery failure could result from a single error, ..." Then, in a Proc. Roy. Soc. London article, he gives five laws for reliable quantum computing, as he reviews the results obtained for avoiding failure. Here, a slightly modified list is discussed. The list is

1. Be careful not to propagate errors,
2. Copy errors not data,
3. Carefully prepare ancilla,
4. Verify ancilla,
5. Verify the syndrome,
6. Take care with measurements.

All of these require some explanation. Let us take them in order.

1. Propagation of Errors

The general statement is that an error should not propagate within a code block and errors should not accumulate. If there is an error probability is $\epsilon \,\!$ for one physical qubit, then the objective is to ensure that the block error is reduced by a power. For protection against one error, the block error should be $\epsilon ^{2}\,\!$, and when encoding against $t\,\!$ errors, the block error should be $\epsilon ^{t+1}\,\!$. If an error propagates within a block, the block error becomes $\epsilon \,\!$ and the encoding has lost all its benefit.

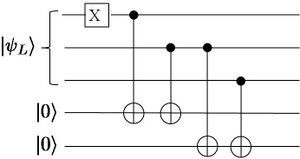
For example, one should be careful when qubits are reused because error correction procedures can actually propagate errors. Consider the syndrome measurement in Figure 7.2. In that circuit, one of the ancillary qubits is used twice to check the parity of a pair of qubits in the bit-flip code. This, however, can propagate a single error in the ancilla to two qubits in the code block. However, this code can only detect and correct one error. Thus such an event would lead to failure.

Figure 7.3

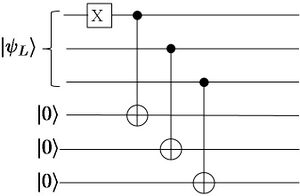
Figure 7.3: Two different syndrome extraction circuits for the three-qubit quantum error correcting code. The figure on the left is not fault-tolerant. It is the same as Figure 7.2. The figure on the right is fault-tolerant. However, as explained in the text, it cannot be used.

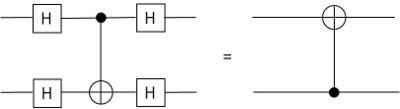
At first this may not seem likely. After all, the target bit is the one that is affected. However, as shown in Figure 7.4 errors can actually propagate from the target to the source, not just from the source to the target, in the CNOT operation.

Figure 7.4

Figure 7.4: The above circuit identity was used by Preskill to show that errors can propagate in not-so-obvious ways. In this particular case, an error can propagate from the source qubit as well as propagating to the target qubit in a CNOT gate.

2. Copy Errors Not Data

The reason we cannot just use one ancilla for each qubit is that this gives information contained in the computation. If all ancilla are measured the superposition of $\alpha \,\!$ and $\beta \,\!$ will be destroyed. This is because the information obtained will result in a $|000\rangle \,\!$ or $|111\rangle \,\!$ state of the system. The data, not just the error, has been extracted leaving classical information.

3. Preparing the Ancilla

In the previous section, the fault-tolerant method extracted too much information. So what can be done? The answer is that a different recovery procedure should be used. Rather than using single qubit ancilla, the ancillary system can composed of several qubits in a special state.

Here are two examples for the Steane code. 1) Shor proposed the state, is one example of the special preparation of an ancilla state which is the superposition of all even weighted strings,

	$|{\mbox{Shor}}\rangle _{\text{anc}}={\frac {1}{\sqrt {8}}}\sum _{{\text{even }}v}|v\rangle _{\text{anc}}.\,\!$	(10.1)

In this case, one computes the syndrome by performing four CNOT gates and then measure the ancilla state. Since the ancilla state is a superposition of all even weighted states, the result will project onto an even weighted string if there is no error and a superposition of add weight states if there is an error. Thus giving the syndrome information. The parity of the ancillary system indicates whether or not there is an error, but without revealing the state of the system.

The second example was given by Steane.

4. Verifying the Ancilla

Since the ancilla is so important, and can propagate an error to the logical qubit (encoded block), it must be carefully prepared and error checked. If there is an error, throw it away and prepare another ancilla.

5. Check the Measurement

	${\begin{aligned}&=\\&=\end{aligned}}\,\!$	(7.?)

Fault-Tolerant Quantum Computing for the Steane Code

$\,\!$