Chapter 2 - Qubits and Collections of Qubits

Introduction

There are several parts to any quantum information processing task. Some of these were written down and discussed by David DiVincenzo in the early days of quantum computing research and are therefore called DiVincenzo’s requirements for quantum computing. These include, but are not limited to, the following, which will be discussed in this chapter. Other requirements will be discussed later.

Five requirements [3]:

1. Be a scalable physical system with well-defined qubits
2. Be initializable to a simple fiducial state such as $\left\vert {000...}\right\rangle$
3. Have much longer decoherence times than gating times
4. Have a universal set of quantum gates
5. Permit qubit-specific measurements

The first requirement is a set of two-state quantum systems which can serve as qubits. The second is to be able to initialize the set of qubits to some reference state. In this chapter, these will be taken for granted. The third concerns noise and noise has become known by the term decoherence. The term decoherence has had a more precise definition in the past, but here it will usually be synonymous with noise. Noise and decoherence will be the topics of later sections. The fourth and fifth will be discussed in this chapter.

Backwards is it? Not from a computer science perspective or from a motivational perspective. Besides, to a large extent, the first two rely very heavily on experimental physics and engineering. These topics are primarily beyond the scope of this introductory material, but will be treated superficially in Chapter 6.

Qubit States

As mentioned in the introduction, a qubit, or quantum bit, is represented by a two-state quantum system. It is referred to as a two-state quantum system, although there are many physical examples of qubits which are represented by two different states of a quantum system which has many available states. These two states are represented by the vectors $\left\vert {0}\right\rangle$ and $\left\vert {1}\right\rangle$ and qubit could be in the state $\left\vert {0}\right\rangle$, or the state $\left\vert {1}\right\rangle$, or a complex superposition of these two. A qubit state which is an arbitrary superposition is written as

	$\left\vert {\psi }\right\rangle =\alpha _{0}\left\vert {0}\right\rangle +\alpha _{1}\left\vert {1}\right\rangle ,$	( 2.1)

where $\alpha _{0}\,\!$ and $\alpha _{1}\,\!$ are complex numbers. Our objective is to use these two states to store and manipulate information. If the state of the system is confined to one state, the other, or a superposition of the two, then

	$|\alpha _{0}|^{2}+|\alpha _{1}|^{2}=1.\,\!$	( 2.2)

Thus this vector is normalized, i.e. it has magnitude, or length one. The set of all such vectors forms a two-dimensional complex (so four-dimensional real) vector space. The basis vectors for such a space are the two vectors $\left\vert {0}\right\rangle$ and $\left\vert {1}\right\rangle$ which are called computational basis states. These two basis states are represented by

	$\left\vert {0}\right\rangle =\left({\begin{array}{c}1\\0\end{array}}\right),\;\;\left\vert {1}\right\rangle =\left({\begin{array}{c}0\\1\end{array}}\right).$	( 2.3)

Therefore,

	$\left\vert {\psi }\right\rangle =\left({\begin{array}{c}\alpha _{0}\\\alpha _{1}\end{array}}\right).$	( 2.4)

Qubit Gates

During a computation, one qubit state will need to be taken to a different one. In fact, any valid state should be able to be operated upon to obtain any other state. Since this is a complex vector with magnitude one, the matrix transformation required for closedsystem evolution is unitary. (See Appendix D, Sec. D.2.) These unitary matrices, or unitary transformations, as well as their generalization to many qubits, transform a one complex vector into another and are also called quantum gates, or gating operations. Mathematically, we may think of them as rotations of the complex vector and in some cases (but not all) correspond to actual rotations of the physical system.

Circuit Diagrams for Qubit Gates

Unitary transformations are represented in a circuit diagram with a box around the untary transformation. Consider a unitary transformation $V$ on a single qubit state $\left\vert {\psi }\right\rangle$. If the result of the transformation is $\left\vert {\psi ^{\prime }}\right\rangle$ then we write

	$\left\vert {\psi ^{\prime }}\right\rangle =V\left\vert {\psi }\right\rangle .$	(2.5)

The corresponding circuit diagram is shown in Fig. 2.1.

Notice that the diagram is read from left to right. This means that if two consecutive gates are implemented, say $V$ first and then $U$, the equation reads

	$\left\vert {\psi ^{\prime \prime }}\right\rangle =UV\left\vert {\psi }\right\rangle .$	(2.6)

$\left\vert {\psi }\right\rangle$

$\left\vert {\psi ^{\prime }}\right\rangle$

Figure 2.1: Circuit diagram for a one-qubit gate which implements the unitary transformation

$V\,\!$. The input state $\left\vert {\psi }\right\rangle$ is on the right and the output, $\left\vert {\psi ^{\prime }}\right\rangle$, is on the right.

However, the circuit diagram will have the boxes in the reverse order from the equation, i.e. $V$ on the left and $U$ on the right.

Examples of Important Qubit Gates

There are, of course, an infinite number of possible unitary transformations that we could implement on a single qubit since the set of unitary transformations can be parameterized by three parameters. However, a single gate will contain a single unitary transformation, which means that all three parameters a fixed. There are several such transformations which are used repeatedly. For this reason, they are listed here along with their actions on a generic state $\left\vert {\psi }\right\rangle =\alpha _{0}\left\vert {0}\right\rangle +\alpha _{1}\left\vert {1}\right\rangle$. Note that one could also completely define the transformation by its action on a complete set of basis states.

The following is called an “x” gate, or a bit-flip,

	$X=\left({\begin{array}{cc}0&1\\1&0\end{array}}\right).$	(2.7)

Its action on a state $\left\vert {\psi }\right\rangle$ is to exchange the basis states,

	$X\left\vert {\psi }\right\rangle =\alpha _{0}\left\vert {1}\right\rangle +\alpha _{1}\left\vert {0}\right\rangle ,$	(2.8)

for this reason it is also sometimes called a NOT gate. However, this term will be avoided because a general NOT gate does not exist for all quantum states. (It does work for all qubit states, but this is a special case.)

The next gate is called a phase gate or a “z” gate. It is also sometimes called a phase-flip, and is given by

	$Z=\left({\begin{array}{cc}1&0\\0&-1\end{array}}\right).$	(2.9)

The action of this gate is to introduce a sign change on the state $\left\vert {1}\right\rangle$ which can be seen through

	$Z\left\vert {\psi }\right\rangle =\alpha _{0}\left\vert {0}\right\rangle -\alpha _{1}\left\vert {1}\right\rangle ,$	(2.10)

The term phase gate is also used for the more general transformation

	$P=\left({\begin{array}{cc}e^{i\theta }&0\\0&e^{-i\theta }\end{array}}\right).$	(2.11)

For this reason, the z-gate will either be called a “z-gate” or a phase-flip gate.

Another gate closely related to these, is the “y” gate. This gate is

	$Y=\left({\begin{array}{cc}0&-i\\i&0\end{array}}\right).$	(2.12)

The action of this gate on a state is

	$Y\left\vert {\psi }\right\rangle =-i\alpha _{1}\left\vert {0}\right\rangle +i\alpha _{0}\left\vert {1}\right\rangle =-i(\alpha _{1}\left\vert {0}\right\rangle -\alpha _{0}\left\vert {1}\right\rangle )$	(2.13)

From this last expression, it is clear that, up to an overall factor of Failed to parse (syntax error): {\displaystyle −i} , this gate is the same as acting on a state with both $X$ and $Z$ gates. However, the order matters. Therefore, it should be noted that

$XZ=-iY,\,\!$

whereas

$ZX=iY.\,\!$

The fact that the order matters should not be a surprise to anyone since matrices in general do not commute. However, such a condition arises so often in quantum mechanics, that the difference between these two is given an expression and a name. The difference between the two is called the commutator and is denoted with a $[\cdot ,\cdot ]$. That is, for any two matrices, $A$ and $B$, the commutator is defined to be

	$[A,B]=AB-BA.\,\!$	(2.14)

For the two gates $X$ and $Z$,

	$[X,Z]=-2iY.\,\!$	(2.15)

A very important gate which is used in many quantum information processing protocols, including quantum algorithms, is called the Hadamard gate,

	$H={\frac {1}{\sqrt {2}}}\left({\begin{array}{cc}1&1\\1&-1\end{array}}\right).$	(2.16)

In this case, its helpful to look at what this gate does to the two basis states:

	$H\left\vert {0}\right\rangle ={\frac {1}{\sqrt {2}}}(\left\vert {0}\right\rangle +\left\vert {1}\right\rangle ),$ $H\left\vert {1}\right\rangle ={\frac {1}{\sqrt {2}}}(\left\vert {0}\right\rangle -\left\vert {1}\right\rangle ).$	(2.17)

So the Hadamard gate will take either one of the basis states and produce an equal superposition of the two basis states. This is the reason it is so-often used in quantum information processing tasks. On a generic state

	$H\left\vert {\psi }\right\rangle =[(\alpha _{0}+\alpha _{1})\left\vert {0}\right\rangle +(\alpha _{0}-\alpha _{1})\left\vert {1}\right\rangle ].$	(2.18)

The Pauli Matrices

The three matrices $X,Y,$ and $Z$ are called the Pauli matrices. They are also sometimes denoted $\sigma _{x}\,\!$, $\sigma _{y}\,\!$ and $\sigma _{z}\,\!$, or $\sigma _{1}\,\!$, $\sigma _{2}\,\!$ and $\sigma _{3}\,\!$ respectively. They are ubiquitous in quantum computing and quantum information processing. This is because they, along with the $2\times 2\,\!$ identity matrix, form a basis for the set of $2\times 2\,\!$ Hermitian matrices and can be used to describe all $2\times 2$ unitary transformations as well. We will return to this latter point in the next chapter.

To show that they form a basis for $2\times 2$ Hermitian matrices, note that any such matrix can be written in the form

	$A=\left({\begin{array}{cc}a_{0}+a_{3}&a_{1}+ia_{2}\\a_{1}-ia_{2}&a_{0}-a_{3}\end{array}}\right).$	(2.19)

Since $a_{0}\,\!$ and $a_{3}\,\!$ are arbitrary, $a_{0}+a_{3}\,\!$ and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 − a_3\,\!} are abitrary too. This matrix can be written as

	${\begin{aligned}A&=a_{0}\mathbb {I} +a_{1}X+a_{2}Y+a_{3}Z\\&=a_{0}\mathbb {I} +a_{1}\sigma _{1}+a_{2}\sigma _{2}+a_{3}\sigma _{3}\\&=a_{0}\mathbb {I} +{\vec {a}}\cdot {\vec {\sigma }},\\\end{aligned}}$	(2.20)

where ${\vec {a}}\cdot {\vec {\sigma }}=\sum _{i=1}^{3}a_{i}\sigma _{i}\,\!$ is the "dot product" beteen ${\vec {a}}\,\!$ and ${\vec {\sigma }}=(\sigma _{1},\sigma _{2},\sigma _{3})\,\!$.

An important and useful relationship between these is the following (which shows why the latter notation above is so useful)

	$\sigma _{i}\sigma _{j}=\mathbb {I} \delta _{ij}+i\epsilon _{ijk}\sigma _{k},$	(2.21)

where $i,j,k\,\!$ are numbers from the set $\{1,2,3\}\,\!$ and the defintions for $\delta _{ij}\,\!$ and $\epsilon _{ijk}\,\!$ are given in Eqs. (D.17) and (D.8) respectively. The three matrices $\sigma _{1},\sigma _{2},\sigma _{3}\,\!$ are traceless Hermitian matrices and they can be seen to be orthogonal using the so-called Hilbert-Schmidt inner product which is defined, for matrices$A\,\!$ and $B\,\!$, as

	$(A,B)={\mbox{Tr}}(A^{\dagger }B).$	(2.22)

The orthogonality for the set is then summarized as

	$(\sigma _{i},\sigma _{j})={\mbox{Tr}}(\sigma _{i}\sigma _{j})=2\delta _{ij}.\,\!$	(2.23)

This property is contained in Eq. (2.21). This one equation also contains all of the commutators. By subtracting the equation with the product reversed

	$[\sigma _{i},\sigma _{j}]=(\mathbb {I} \delta _{ij}+i\epsilon _{ijk}\sigma _{k})-(\mathbb {I} \delta _{ji}+i\epsilon _{jik}\sigma _{k}),$	(2.24)

but $\delta _{ij}=\delta _{ji}\,\!$ and $\epsilon _{ijk}=-\epsilon _{jik}\,\!$ so

	$[\sigma _{i},\sigma _{j}]=2i\epsilon _{ijk}\sigma _{k}.\,\!$	(2.25)

States of Many Qubits

Let us now consider the states of several (or many) qubits. For one qubit, there are two possible basis states, say $\left\vert {0}\right\rangle \,\!$ and $\left\vert {1}\right\rangle \,\!$. If there are two qubits, each with these basis states, basis states for the two together are found by using the tensor product. (See Section D.6.) The set of basis states obtained in this way is

$\left\{\left\vert {0}\right\rangle \otimes \left\vert {0}\right\rangle ,\;\left\vert {0}\right\rangle \otimes \left\vert {1}\right\rangle ,\;\left\vert {1}\right\rangle \otimes \left\vert {0}\right\rangle ,\;\left\vert {1}\right\rangle \otimes \left\vert {1}\right\rangle \right\}.\,\!$

This set is more often written as

	$\left\{\left\vert {00}\right\rangle ,\;\left\vert {01}\right\rangle ,\;\left\vert {10}\right\rangle ,\;\left\vert {11}\right\rangle \right\},\,\!$	(2.26)

which can also be expressed as

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right), \; \left(\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right), \; \left(\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right), \; \left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right) \right\}.\,\!}	(2.27)

The extension to three qubits is straight-forward

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{\left\vert{000}\right\rangle, \; \left\vert{001}\right\rangle, \; \left\vert{010}\right\rangle, \; \left\vert{011}\right\rangle, \; \left\vert{100}\right\rangle, \; \left\vert{101}\right\rangle, \; \left\vert{110}\right\rangle, \; \left\vert{111}\right\rangle \right\}.\,\!}	(2.28)

Those familiar with binary will recognize these as the numbers zero through seven. Thus we consider this an ordered basis with the following notation also perfectly acceptable

	$\left\{\left\vert {0}\right\rangle ,\;\left\vert {1}\right\rangle ,\;\left\vert {2}\right\rangle ,\;\left\vert {3}\right\rangle ,\;\left\vert {4}\right\rangle ,\;\left\vert {5}\right\rangle ,\;\left\vert {6}\right\rangle ,\;\left\vert {7}\right\rangle \right\}.\,\!$	(2.29)

The ordering of the products is important because each spot corresponds to a physical particle or physical system. When some confusion may arise, we may also label the ket with a subscript to denote the particle or position. For example, two different people, Alice and Bob, can be used to represent distant parties which may share some information or may wish to communicate. In this case, the state belonging to Alice may be denoted Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{\psi}\right\rangle_A\,\!} . Or if she is referred to as party 1 or particle 1, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{\psi}\right\rangle_1\,\!} .

The most general 2-qubit state is written as

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{\psi}\right\rangle = \alpha_{00}\left\vert{00}\right\rangle + \alpha_{01}\left\vert{01}\right\rangle + \alpha_{10}\left\vert{10}\right\rangle + \alpha_{11}\left\vert{11}\right\rangle =\left(\begin{array}{c} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{array}\right).}	(2.30)

The normalization condition is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_{00}|^2 + |\alpha_{01}|^2 + |\alpha_{10}|^2 + |\alpha_{11}|^2=1.\,\!} The generalization to an arbitrary number of qubits, say $n$, is also rather straight-forward and can be written as

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{\psi}\right\rangle = \sum_{i=0}^{2^n-1} \alpha_i\left\vert{i}\right\rangle.\,\!}

Quantum Gates for Many Qubits

Just as the case for one single qubit, the most general closed-system transformation of a state of many qubits is a unitary transformation. Being able to make an abitrary unitary transformation on many qubits is an important task. If an arbitrary unitary transformation on a set of qubits can be made, then any quantum gate can be implemented. If this ability to implement any arbitrary quantum gate can be accomplished using a particular set of quantum gates, that set is said to be a universal set of gates or that the condition of universality has been met by this set. It turns out that there is a theorem which provides one way for identifying a universal set of gates.

Theorem:

The ability to implement an entangling gate between any two qubits, plus the ability to implement all single-qubit unitary transformations, will enable universal quantum computing.

It turns out that one doesn’t need to be able to perform an entangling gate between distant qubits. Nearest-neighbor interactions are sufficient. We can transfer the state of a qubit to a qubit which is next to the one we would like it to interact with. Then perform the entangling gate between the two and then transfer back.

This is an important and often used theorem which will be the main focus of the next few sections. A particular class of two-qubit gates which can be used to entangle qubits will be discussed along with circuit diagrams for many qubits.

Controlled Operations

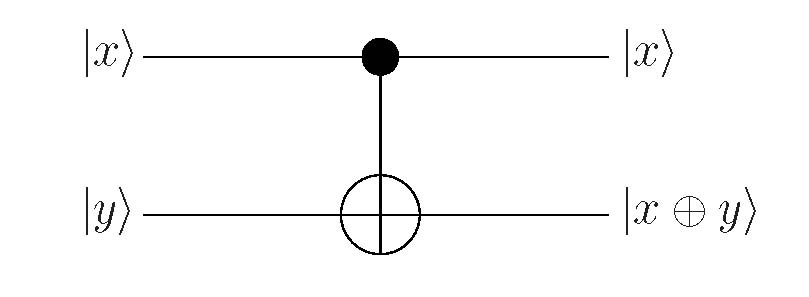
A controlled operation is one which is conditioned on the state of another part of the system, usually a qubit. The most cited example is the CNOT gate, which is a NOT operation on one qubit that is implemented only if another qubit is in the state $\left\vert {1}\right\rangle \,\!$, in other words a controlled NOT operation. This gate is used so often that it is discussed here in detail.

Consider the following matrix operation on two qubits

	$C_{12}=\left({\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{array}}\right).$	(2.31)

Under this transformation, the following changes occur:

	${\begin{array}{c|c}\;\left\vert {\psi }\right\rangle \;&C_{12}\left\vert {\psi }\right\rangle \\\hline \left\vert {00}\right\rangle &\left\vert {00}\right\rangle \\\left\vert {01}\right\rangle &\left\vert {01}\right\rangle \\\left\vert {10}\right\rangle &\left\vert {11}\right\rangle \\\left\vert {11}\right\rangle &\left\vert {10}\right\rangle \end{array}}$	(2.32)

This transformation is called the CNOT, or controlled NOT, since the second bit is flipped if the first is in the state $\left\vert {1}\right\rangle \,\!$, and otherwise left alone. The circuit diagram for this transformation corresponds to the following representation of the gate. Let $x\,\!$ and $y\,\!$ be zero or one. Then the CNOT is given by

	$\left\vert {x,y}\right\rangle {\overset {CNOT}{\rightarrow }}\left\vert {x,x\oplus y}\right\rangle .$	(2.33)

In binary, of course $0\oplus 0=0$, $0\oplus 1=1=1\oplus 0$, and $1\oplus 1=0$. The circuit diagram is given in Fig. 2.2. The first qubit, $\left\vert {x}\right\rangle$, at the top of the diagam, is called the control bit and the second, $\left\vert {y}\right\rangle$, at the top of the diagam, is called the target bit.

$\left\vert {X}\right\rangle \,\!$

$\left\vert {Y}\right\rangle \,\!$

Figure 2.2: Circuit diagram for a CNOT gate.

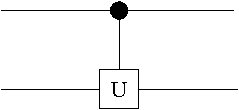
One can immediately generalize the operation of the CNOT to a controlled-U gate. This is a gate, shown in Fig. 2.3, which implements a unitary transformation $U\,\!$ on the second qubit, if the state of the first is $\left\vert {1}\right\rangle \,\!$. The matrix transformation is given by

	$CU_{12}=\left({\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&u_{11}&u_{12}\\0&0&u_{21}&u_{22}\end{array}}\right),$	(2.34)

where the matrix

$U=\left({\begin{array}{cc}u_{11}&u_{12}\\u_{21}&u_{22}\end{array}}\right).$

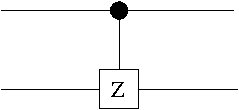
For example the controlled-phase gate is given in Fig. 2.4.

Figure 2.3: Circuit diagram for a CU gate.

Many-qubit Circuits

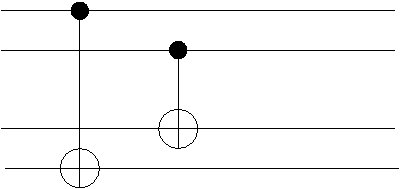
Many qubit circuits are a straight-forward generalization of the single quibit circuit diagrams. For example, Fig. 2.5 shows the implementation of CNOT$_{14}$ and CNOT$_{23}$ in the same diagram. The crossing of lines is not confusing since there is a target and control which are clearly distinguished in each case.

It is quite interesting however, that as the diagrams become more complicated, the possibility arises that one may change between equivalent forms of a circuit which, in the end,

Figure 2.4: Circuit diagram for a Controlled-phase gate.

Figure 2.5: Multiple CNOT gates on a set of qubits.

implements the same multiple-qubit unitary. For example, noting that $HZH=X\,\!$, the two circuits in Fig. 2.6 implement the same two-qubit unitary transformation. This enables the simplication of some quite complicated circuits.

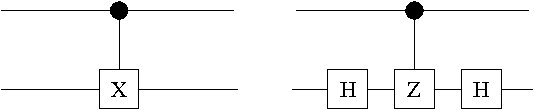
Figure 2.6: Two circuits which are equivalent since they implement the same two-qubit unitary transformation.

Measurement

Measurement in quantum mechanics is quite different from that of classical mechanics. In classical mechanics, and therefore for classical bits in classical computers, one assumes that a measurement can be made at will without disturbing or changing the state of the physical system. In quantum mechanics this assumption cannot be made. This is important for a variety of reasons which will become clear later.

Standard Prescription

In the intoduction a simple example was provided as motivation for distinguishing quantum states from classical states. This example of two wells with one particle, can be used (cautiously) here as well.

Consider the quantum state in a superposition of $\left\vert 0\right\rangle \,\!$ and $\left\vert 1\right\rangle \,\!$ of the form

	$\left\vert \psi \right\rangle =\alpha _{0}\left\vert 0\right\rangle +\alpha _{1}\left\vert 1\right\rangle ,\,\!$	(2.35)

with $|\alpha _{0}|^{2}+|\alpha _{1}|^{2}=1\,\!$. If the state is measured in the computational basis, the result will be $\left\vert 0\right\rangle \,\!$ with probability $|\alpha _{0}|^{2}\,\!$ and $\left\vert 1\right\rangle \,\!$ with probability $|\alpha _{1}|^{2}\,\!$. Recall that the particle is in this state and that this state really means that the particle is not in the state $\left\vert 0\right\rangle \,\!$ or the state $\left\vert 1\right\rangle \,\!$, it really means that it is in both at the same time.

This is worth emphasizing since it really cannot be thought of as being in state $\left\vert 0\right\rangle \,\!$ with probability $|\alpha _{0}|^{2}\,\!$ or in $\left\vert 1\right\rangle \,\!$ with probability $|\alpha _{1}|^{2}\,\!$. If it were then one could act on the state with a Hadamard transformation and there would be some probability of it being in $\left\vert 0\right\rangle \,\!$ and some probability of being in $\left\vert 1\right\rangle \,\!$. However, acting on the state $\left\vert \psi \right\rangle \,\!$ with a Hadamard transformation,

	$H\left\vert \psi \right\rangle =\left\vert 0\right\rangle .\,\!$	(2.36)

This state has probability zero of being in the state $\left\vert 1\right\rangle \,\!$ and probability one of being in the state $\left\vert 0\right\rangle \,\!$. (This argument is so simple and pointed, that I lifted it directly from Mermin's book {Mermin:book}, page 27.)

A measurement in the computational basis is said to project this state into either the state $\left\vert 0\right\rangle \,\!$ or the state $\left\vert 1\right\rangle \,\!$ with probabilities $|\alpha _{0}|^{2}\,\!$ and $|\alpha _{1}|^{2}\,\!$ respectively. To understand this as a projection, consider the following way in which the $0\,\!$-component of the state $\left\vert \psi \right\rangle \,\!$ is found. The state $\left\vert \psi \right\rangle \,\!$ is projected onto the the state $\left\vert 0\right\rangle \,\!$ mathematically by taking the inner product of $\left\vert 0\right\rangle \,\!$ and $\left\vert \psi \right\rangle \,\!$

	$\left\langle 0\mid \psi \right\rangle =\alpha _{0}.\,\!$	(2.37)

Notice that this is a complex number and that its complex conjugate can be expressed as

	$\left\langle \psi \mid 0\right\rangle =\alpha _{0}^{*}.\,\!$	(2.38)

Therefore the probability can be expressed as

	$\left\langle \psi \mid 0\right\rangle \left\langle 0\mid \psi \right\rangle =\left\vert \left\langle 0\mid \psi \right\rangle \right\vert ^{2}.\,\!$	(2.39)

Now consider a multiple-qubit system with state

	$\left\vert \Psi \right\rangle =\sum _{i}\alpha _{i}\left\vert i\right\rangle .\,\!$	(2.40)

The result of a measurement is a projection and the state is projected onto the state $\left\vert i\right\rangle \,\!$ with probability $|\alpha _{i}|^{2}\,\!$ and the same properties are true of this more general system.

To summarize, if a measurement is made on the system $\left\vert \Psi \right\rangle \,\!$, the result $\left\vert i\right\rangle \,\!$ is obtained with probability $|\alpha _{i}|^{2}\,\!$. Assuming that $\left\vert i\right\rangle \,\!$ results from the measurement, the state of the system has been projected into the state $\left\vert i\right\rangle \,\!$. Therefore, the state of the system immediately after the measurement is $\left\vert i\right\rangle \,\!$.

A circuit diagram with a measurement represented by a box with an arrow is given in Fig.~\ref{fig:measex}. In this case, the measurement result is used for input for another state. The unitary in this diagram is one that depends upon the outcome of the measurement. Notice that the information input, since it is classical, is represented by a double line.

Projection Operators

Projection operators are used quite often and the description of measurement in the previous section is a good example of how they are used. One may ask, what is a projecter? In ordinary three-dimensional space, a vector is written as ${\vec {v}}=v_{x}{\hat {x}}+v_{y}{\hat {y}}+v_{z}{\hat {z}}\,\!$ and the $x\,\!$ part of the vector can be obtained by

	${\hat {x}}({\hat {x}}\cdot {\vec {v}})=v_{x}{\hat {x}}.\,\!$	(2.40)

This is the part of the vector lying along the x axis. Notice that if the projection is performed again, the same result is obtained

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{x}(\hat{x} \cdot v_x\hat{x}) = v_x\hat{x}.\,\!}	(2.41)

This is (the) characteristic of projection operations. When one is performed twice, the second result is the same as the first.

This can be extended to the complex vectors in quantum mechanics. The outter product Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{x}\right\rangle\!\!\left\langle{x}\right\vert\,\!} is a projecter. For example, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\vert{0}\right\rangle\!\!\left\langle{0}\right\vert\,\!} is a projecter and can be written in matrix form as

$\left\vert {0}\right\rangle \!\!\left\langle {0}\right\vert =\left({\begin{array}{cc}1&0\\0&0\end{array}}\right).\,\!$

Acting with this on Failed to parse (unknown function "\ket"): {\displaystyle \ket{\psi} = \alpha_0\left\vert{0}\right\rangle + \alpha_1\left\vert{1}\right\rangle\,\!} gives

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right) \left(\begin{array}{c} \alpha_0 \\ \alpha_1 \end{array}\right) = \left(\begin{array}{c} \alpha_0 \\ 0 \end{array}\right). \,\!}

Acting again produces

$\left({\begin{array}{cc}1&0\\0&0\end{array}}\right)\left({\begin{array}{c}\alpha _{0}\\0\end{array}}\right)=\left({\begin{array}{c}\alpha _{0}\\0\end{array}}\right).\,\!$

This is due to the fact that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\left\vert{0}\right\rangle\!\!\left\langle{0}\right\vert)^2 = \left\vert{0}\right\rangle\!\!\left\langle{0}\right\vert. \,\!}

In fact this property essentially defines a project. A projection is a linear transformation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P\,\!<math> such that <math>P^2 = P\,\!<math>. \index{projection operator} Much of our intuition about geometric projections in three-dimensions carries to the more abstact cases. One important example is that the sum over all projections is the identity. (See also Appendix \ref{app:alg}, Sec.~\ref{sec:MDirac}.) The generalization to arbitrary dimensions, where <math>\ket{i}\,\!<math> is any basis vector in that space, is immediate. In this case the identity, expressed as a sum over all projecters, is <math> \sum_{\mbox{\scriptsize all}\; i} \left\vert{i}\right\rangle\!\!\left\langle{i}\right\vert = 1. \,\!}