Appendix B - Complex Numbers

Complex numbers arise naturally from an attempt to solve the equation

$a^{2}+1=0.\,\!$

It's easy enough to write such an equation down, but how would you solve it? The answer is

$a=\pm {\sqrt {-1}}=\pm i.\,\!$

We let the symbol $i\,\!$ represent ${\sqrt {-1}}\,\!$, so that $i^{2}=-1\,\!$. Then any number of the form

	$z=x+iy,\,\!$	(B.1)

where $x\,\!$ and $y\,\!$ are real is called a complex number. Complex numbers arise in a variety of applications, including quantum mechanics. Suppose we have two complex numbers to be $z_{1}=x_{1}+iy_{1}\,\!$ and $z_{2}=x_{2}+iy_{2}\,\!$. Then the two complex numbers are equal,

$z_{1}=z_{2}.\,\!$

This means that

$x_{1}+iy_{1}=x_{2}+iy_{2},\,\!$

is true if and only if

$x_{1}=x_{2},\;\;{\mbox{ and }}\;\;y_{1}=y_{2}.\,\!$

We refer to $x\,\!$ as the real part of the complex number $z\,\!$ and $y\,\!$ as the imaginary part. Sometimes these are written as Re($z\,\!$) and Im($z\,\!$) respectively. That is, $x=\,\!$Re($z\,\!$) and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\,\!} Im(Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\,\!} ).

We may restate the equivalence condition as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1=z_2\,\!} if and only if the real part of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1\,\!} is equal to the real part of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2\,\!} and the imaginary part of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1\,\!} is equal to the imaginary part of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2\,\!} .

To add two complex numbers, add the real parts and the imaginary parts separately:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1 + z_2 = (x_1+iy_1) + (x_2+iy_2) = (x_1 + x_2) + i(y_1 + y_2). \,\!}

Complex numbers are multiplied like any other binomial expression (recall FOIL: First two, Outside two, Onside two, Last two):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} z_1z_2 &= (x_1+iy_1)(x_2+iy_2) \\ &= x_1x_2 + iy_1x_2 + ix_1y_2 - y_1y_2 \\ &= x_1x_2 - y_1y_2 +i(y_1x_2 + x_1y_2), \end{align}\,\!}

where we have used Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2 = -1\,\!} .

The complex conjugate of the complex number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\,\!} is denoted Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^*\,\!} and is given by

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^* = x-iy. \,\!}	(B.2)

Taking the complex conjugate of the number means just changing the sign in front of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\,\!} . One reason for defining this is that a number times its own complex conjugate is real,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle zz^* = (x+iy)(x-iy) = x^2 + y^2 +i(xy - yx) = x^2 +y^2. \,\!}

The complex conjugate of the complex conjugate is the original complex number, and

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^*z = (x-iy)(x+iy) = x^2 + y^2 +i(yx - xy) = x^2 +y^2 = zz^*. \,\!}

We also call this the modulus squared . The modulus is

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z| = \sqrt{(z^*z)} = \sqrt{x^2 + y^2}. \,\!}	(B.3)

Note that the complex conjugate of a product is the product of the complex conjugates:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (z_1z_2)^* = z_1^* z_2^*. \,\!}

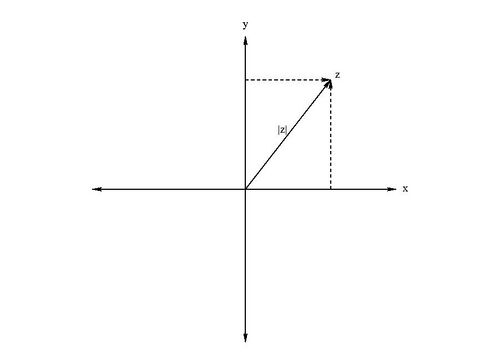
It is often useful to look at a graph for a complex number, consisting of an x-axis for the real part and a y-axis for the complex part. This is shown in Fig. B.1. In this way, we can think of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\,\!} as a two-dimensional vector with the magnitude (length) being equivalent to the modulus of the complex number, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z| = \sqrt{x^2 + y^2}\,\!} . In some sense (like looking at the complex number as a vector), the modulus of the complex number is the length, or magnitude, of the complex number.

Figure B.1: A complex number in Cartesian coordinates.

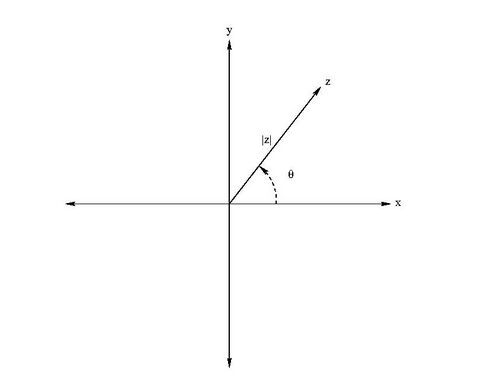
Another useful way to represent this is with polar coordinates. We can do this by writing

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = |z|(\cos\theta +i \sin\theta). \,\!}

Clearly if we wanted to rewrite this in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y\,\!} , we find that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=|z|\cos\theta\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = |z|\sin\theta\,\!} .

A very famous identity exists between the exponential function and sine and cosine,

	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta} = \cos\theta + i \sin\theta, \,\!}	(B.4)

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e\,\!} is the exponential function, which is a number that is approximately 2.71828. Using this equation, we could also write

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = |z|e^{i\theta}. \,\!}

This is really just a short-hand notation for us and most of the time, when we calculate something, we will use the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin\theta, \cos\theta\,\!} functions. But is often the case that people will write this as

	$z=re^{i\theta },\,\!$	(B.5)

where $r={\sqrt {x^{2}+y^{2}}}\,\!$ as is usual for polar coordinates. So everything is just like polar coordinates with the exception of the inclusion of the factor $i\,\!$. (See Fig. B.2.)

Figure B.2: A polar coordinate representation of a complex number.

Exercises

Let $z_{1}=5+2i\,\!$ and $z_{2}=3+i\,\!$. For 2-6, write the answer in terms of the real and complex components, i.e., in the form $x+iy\,\!$, where $x\,\!$ and $y\,\!$ are real numbers.

1. Find $x$ using the quadratic equation: $\;\;{\frac {1}{2}}x^{2}-x+1=0\,\!$
2. What is $z_{1}+z_{2}\,\!$?
3. What is $z_{1}-z_{2}\,\!$?
4. Calculate $z_{1}z_{2}^{*}\,\!$
5. What is $3z_{1}\,\!$?
6. Find $|z_{1}|\,\!$.
7. Find $|z_{2}|^{2}\,\!$.
8. Write $z_{1}\,\!$ as Equation (B.5) using Equation (B.4).

Further Problems:

1. Show that $|z_{1}z_{2}|=|z_{1}||z_{2}|\,\!$
2. Show that $(z_{1}z_{2})^{*}=z_{1}^{*}z_{2}^{*}\,\!$