Chapter 1 - Introduction

Introduction

In science one tries to tell people, in such a way as to be understood by everyone, something that no one ever knew before. But in poetry, it's the exact opposite.

-Paul Dirac

An Introduction to Quantum Computation

This introductory chapter is a survey of, and introduction to, topics in quantum information processing. All of these topics (and more) will be revisited in later sections. Therefore, it is not necessary, nor expected, that these topics will be completely explained in this introductory material.

Quantum Computing

A quantum computer would be a computer that take advantage of quantum mechanical principles according to which physical systems behave. We often think of quantum mechanics as being the set of mechanical laws or principles that very small particles obey. While this is not entirely true, it is a somewhat reasonable way of explaining things to the layman. For our purposes, we should note that everything obeys the laws of quantum mechanics and that Newtonian mechanics are rules that we use to approximate quantum mechanics. However, quantum mechanical control and natural quantum mechanical evolution are what we are talking about when we talk about quantum systems. We must have quantum mechanical evolution, which cannot be reasonably approximated with classical mechanics, and use it in a particular way to really perform a quantum computation or to really do quantum information processing.

So what is quantum mechanics? We should think of it as a set of rules, in some ways similar to Newton’s laws, which describe the way the world works. These are the rules to which we must carefully attend in order to build what we will describe as a quantum computing device. We will return to this topic briefly again later. However, as is done in many places, this question is never quite answered directly. Most often we simply learn the rules and how use them. The question itself is perhaps a little vague because there are many physical systems that don’t quite fit into an either/or categorization of quantum vs. classical. Also, it should noted that throughout these notes the terms will be somewhat misused in the sense that certain systems will be called quantum mechanical or classical, and from now on, with few exceptions, no care will be taken to discuss subtleties.

We have not yet built a quantum computing device. However, there are many reasons to study quantum information processing other than building a fully functional quantum computer. One main reason we haven’t built one is that we have to figure out how. The experiments to perform quantum computation in physical devices take an enormous amount of effort due to noises which corrupt the information. We are going to need to fix the corrupted information, avoid the noises, or do away with them by some other means. A second reason to study quantum computing, and quantum information processing more generally, is that there are really many quantum information processing tasks, or tasks which can be thought of in this way, which concern quantum control. Precise control of a quantum system is important for a variety of reasons, not the least of which is that our world is quantum mechanical! When we get right down to the very basic elements of the universe, they behave quantum mechanically. If there is one thing that the study of quantum information processing has already taught us, its that we need to pay attention to quantum mechanics because it can be very useful to be able to manipulate quantum systems and take advantage of uniquely quantum properties. Quantum technologies are going to be extremely important in the future, even if we never built a quantum computer. (Oh, but we will!) As Feynman said, “There is plenty of room at the bottom.” We have a lot to discover about the world of the small.

Since noise has been, and is still, such a problem for quantum information, we need to deal with it. I started learning about these things in 2000, and I would attribute most of what I know about the subject to Daniel Lidar, whether it be direct or indirect. He was one of the first people to realize the importance of attacking the problem whole-heartedly. People recognized the problem, and Shor, et al. really made remarkable statements with their work on quantum error correcting codes. This work showed that errors could, in principle, be corrected, leading the way for future research since it was now plausible that a quantum computer could be built – there are no fundamental obstacles. However, quantum error correcting codes are, in some sense, a software solution to a hardware problem. More physical treatments include decoherence-free subspaces, (and noiseless subsystems) and dynamical decoupling. However, an all-out attack will include other methods of error prevention. Error prevention methods, as I call all of these along with combinations, are the subject of the last part of this course/book for that reason.

Motivation

Why do we want to build a quantum computing device?

1. To make computers faster and more compact, we have been making them smaller.(This has obeyed Moore’s law. (ref.)) However, there is a limit to how much smaller we can make them, and still have them function as they do now. This is due to quantum mechanics. The limit to small is quantum mechanics – quantum mechanics starts to become the dominate mechanism by which constituents interact. So, to make things smaller, we need to use quantum mechanics! More than this though, the fact that Moore’s law cannot continue indefinitely means that we will need to look elsewhere for advances in computing power. One way to increase computing power is to parallelize computations. However, there are processes which cannot be parallelized. So where do we turn? A quantum computer would help with this.
2. We now know of several different quantum algorithms which are faster than any known classical algorithm for performing the same task. Some are actually provably faster. These are listed and discussed futher in the next section.
3. Quantum information can be used in a variety of ways beyond computing. Such as quantum cryptography, quantum games, and quantum communication of all sorts. (Use Carl’s notes here and cite them (ref.))

An important point to take away from this section is that information is stored and manipulated by physical devices. They way in which they behave is important for the tasks that are to be performed.

Specific Uses

There are three advantages of quantum computing devices which are often quoted.

1. Factor large integers efficiently (known as Shor’s algorithm)
2. Find an object in an unsorted database more efficiently than a classical machine (known as Govers algorithm, e.g. phone number lookup)
3. Simulate quantum mechanical systems more efficiently than any classical system (due to Feynman and others)

COMMENTS

Shor’s algorithm would render RSA encryption useless. It is more efficient than any known classical algorithm. (There is a quantum answer to this problem however-quantum cryptography through QKD.)

Gover’s algorithm is better than any classical algorithm – phone book example: classical algorithm grows as N/2 and Grover’s grows as sqrt N

Simulating quantum mechanical systems is quite difficult classically. For physical scientists this could be the most important application of quantum computers. This could enable the simulation of nuclear systems, solid-state devices, biological molecules and molecular interactions, etc.

How do quantum computers provide an advantage?

Now, the claim is that quantum computers could solve some problems more efficiently than classical ones. So viewing our information systems as quantum systems, we may note that quantum mechanics is more than a description of the physical world (which is how physicists treated it for years) but a set of rules governing the behaviour of information when stored and manipulated quantum mechanically.

So the natural question is, “How does it do this?” We may also ask, “Where is the advantage?” In other words, “What exactly about quantum mechanics enables us to achieve speed-ups and other information processing tasks more efficiently than classical systems?” Most people, as of the time of this writing, would likely say they don’t know. For example, it is not known if there is a classical algorithm which could factor efficiently. (By efficiently here, let us just say that we mean “as well as a quantum one.” We'll be more specific later. ) So what I will discuss is what I would call intuitive arguments for why be believe a quantum computer can accomplish things a classical one cannot. We should not claim this is proof of anything at this point.

The first argument is that when a machine has different rules for operating, we expect it to do different things. The rules by which classical computing machines function are, in some sense, different from the ones governing the behaviour of quantum machines. This is quite vague, especially given the earlier comments about how everything really is quantum mechanical. The way I think about it (you’re welcome to argue) is that a “classical object” transforms according to a “classical equation of motion” ∗ and the result is determined by its initial state, which is “classical.” A quantum mechanical state transforms according to a “quantum equation of motion” and the result of the evolution is determined by some initial conditions, which describe a “quantum system.” Perhaps this sounds like a circular argument, primarily involving semantics. However, my motivation for this is a definition I was given in a vector and tensor analysis class: an object is a tensor if it transforms like a tensor. So I say, an object is classical if it obeys classical equations. In practice, this is often the way things are done. If the physical system can be approximated using classical mechanics, it is classical.

The next argument is that there are states which are uniquely quantum mechanical. These are states which would have been mysterious to Newton, and indeed they were mysterious to Einstein, and furthermore they are still mysterious today! The important point is that they are not states of classical systems, i.e. they are not states which behave classically. They are unique to quantum mechanics and are called entangled states. Let us first discuss bits and qubits. We will then discuss quantum states of many particles which correspond to entangled states. Finally, we will revisit this notion of intuition behind the quantum mechanical speed-ups.

Bits and qubits: An Introduction

A classical bit is represented by two different states of a classical system. In classical computers it is represented by two different values of an electrical potential difference. The two different states of the system are represented by 0 and 1.

A quantum bit or qubit (better, but less used is Qbit, see [11]) is represented by two states of a quantum mechanical system. The two different states are represented by $\left\vert {0}\right\rangle$ and $\left\vert {1}\right\rangle$. This notation is common and is explained in some detail in Appendix D.

Figure 1.1: This is a double well with a ball in one of the two wells.

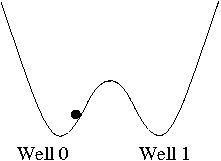
Let us discuss a way in which to think about the differences between classical and quantum systems. We will consider two wells, or valleys, with a hill in between as in Fig. 1.1. First we will consider a classical system and we will suppose there are no frictional forces. If we start the ball rolling where it is in the figure, then it will roll back and forth in Well 0. (Well 0, or “Well zero” is our name for the well on the left-hand side.) It will never leave Well 0 if we leave it alone. If we wanted it to go into Well 1 (the well on the right-hand side) we would need to nudge it or push it a little to get it over the hill. Or we could just pick it up and move it from one well to the other.

Now suppose the system is quantum mechanical. In this case, if we set up the system so that the particle initially has some kinetic energy (imagine a moving “quantum ball”), and let it go, there is some probability, after some amount of time, that the particle will be found in Well 1. This is true when the energy of the ball was not great enough to travel over the hill in the classical analogy. The probability if it being found in the other well depends on several things; the initial energy of the particle, the width of the hill, and the height of the hill (equivalently the depth(s) of the wells, which could be different). However, it won’t happen classically! So this is a difference between the classical and quantum mechanics. In quantum mechanics, the particle is in some sense in both wells at the same time. This has to do with the “wave” nature of quantum mechanics. We then say that the particle is in a superposition of Well 0 and Well 1 and the same time. Mathematically, we describe these different physical “states” or conditions of the system in the following way.

	Particle is in Well $0=\left\vert {0}\right\rangle$, Particle is in Well $1=\left\vert {1}\right\rangle$	(1.1)

In other words, the state of the system is “the particle is in Well 0” is written mathematically as $\left\vert {0}\right\rangle$, and simiarly for $\left\vert {1}\right\rangle \,\!$. If the particle is in a superposition of the two, which will mean some probability for finding in each well, we would write this as

	$\left\vert {\psi }\right\rangle =\alpha \left\vert {0}\right\rangle +\beta \left\vert {1}\right\rangle \,\!$	(1.2)

where $\alpha \,\!$ and $\beta \,\!$ are complex numbers (see Appendix D) and the probability of the particle being found in Well 0 is $|\alpha |^{2}\,\!$ and the probability of it being found in Well 1 is $|\beta |^{2}\,\!$.

Now, some (physicists no less) have asked how to make a deterministic transformation in a quantum system. After all, this seems to be probablistic. The way to do that is the following. We make the hill very wide and tall and we put the particle right down in the bottom of one well and give it as little initial energy as possible. Then if we want it moved to the other well, we pick it up and move it.

If we measure the system, i.e. look to see if it is Well 0 or Well 1, we will “project it into one state or the other.” In other words, suppose the system is in the state |ψi above. If we look to see where the particle is and find it in Well 1, then the probability is clearly zero that it is in the other one. This is called the projection postulate in quantum mechanics and we will see how to represent this mathematically later.

Throughout the notes, when trying to think about a physical qubit, this simple picture is often good enough. Therefore, we will refer back to it from time to time.

NOTE: Don’t forget to add the “intuition” part.

Obstacles to Building a Reliable Quantum Computer

Noise is the greatest obstacle to building a quantum computer. This was also the case with early electronic classical computing devices. In this case there is an intuitive explanation ...

For our purposes, we will need to discuss open-system evolution and closed-system evolution. A closed system is one which does not have any interaction with external objects. We may also refer to such a system as isolated. For example, one knows that if a jar has a very good lid on it, no liquid can leak out, or into, the jar. So if we put a certain amount of liquid in it now, we can expect it will all be there later. This is a closed system and the liquid is isolated from masses external to the jar. In other words, no other mass can get in or out.

A better example is what we call thermally isolated, meaning no heat energy is exchanged with any other system, so this is a thermally closed system. An open system is one which can interact with its environment in some way. In these examples, a lid that is not sealed can allow liquid vapors to escape and one that is not thermally isolated, or thermally closed can heat up or cool down.

For the quantum information processing tasks we have in mind, we will consider quantum information which is isolated form its environment and what we usually mean is that the quantum system is isolated and cannot be affected by an outside source. It is important to note that isolated, or closed systems, are ideal. They may often be good approximations to a system, but are basically never really completely isolated or closed.

One may consider larger and larger systems to try to obtain a closed system, but this is most often impractical, although it can be useful for modeling.