Chapter 2 - Qubits and Collections of Qubits
Contents
Introduction
There are several parts to any quantum information processing task. Some of these were written down and discussed by David DiVincenzo in the early days of quantum computing research and are therefore called DiVincenzo’s requirements for quantum computing. These include, but are not limited to, the following, which will be discussed in this chapter. Other requirements will be discussed later. The following are some basic requirements for any scalable quantum computing system.
Five requirements DiVincenzo:2000 [7]:
- Be a scalable physical system with well-defined qubits
- Be initializable to a simple fiducial state such as
- Have much longer decoherence times than gating times
- Have a universal set of quantum gates
- Permit qubit-specific measurements
The first requirement is a set of two-state quantum systems which can serve as qubits. The second is to be able to initialize the set of qubits to some reference state. In this chapter, these will be taken for granted. The third concerns noise or as it has become known, "decoherence." The term decoherence has had a more precise definition in the past, but here it will usually be synonymous with noise. Noise/decoherence will be discussed in Chapter 6. This chapter is primarily concerned with the fifth of these criteria. This will enable us to discuss many interesting aspects of quantum information problems while postponing some other technical details regarding the other criteria. In addition, we cannot ignore the fifth requirement since it also concerns universality which is the ability to perform an arbitrary computation.
Qubit States
As mentioned in the introduction, a qubit, or quantum bit, is represented by a two-state quantum system. It is referred to as a two-state quantum system, although there are many physical examples of qubits which are represented by two different states of a quantum system that has many available states. These two states are represented by the vectors and and the qubit could be in the state , the state , or a complex superposition of these two. A qubit state which is an arbitrary superposition is written as
| (2.1) |
where and are complex numbers. Our objective is to use these two states to store and manipulate information. If the state of the system is confined to one state, the other state, or a superposition of the two, then
| (2.2) |
This means that this vector is normalized, i.e. its magnitude (or length) is one. The set of all such vectors forms a two-dimensional complex (so four-dimensional real) vector space. (Appendix B contains a basic introduction to complex numbers.) The basis vectors for such a space are the two vectors and which are called computational basis states. These two basis states are represented by
| (2.3) |
Thus, the qubit state can be rewritten as
| (2.4) |
Qubit Gates
During a computation, one qubit state will need to be taken to a different one. In fact, any valid state should be able to be operated upon to obtain any other state. Since this is a complex vector with magnitude one, the matrix transformation required for closed system evolution is unitary (see Appendix C.3.9, Unitary Matrices). These unitary matrices, or unitary transformations, as well as their generalization to many qubits, transform one complex vector into another and are also called quantum gates, or gating operations. Mathematically, we may think of them as rotations of the complex vector and in some cases (but not all) correspond to actual rotations of the physical system.
Circuit Diagrams for Qubit Gates
Unitary transformations are represented in a circuit diagram with a box around the unitary transformation. Consider a unitary transformation on a single qubit state . If the result of the transformation is , we can then write
| (2.5) |
The corresponding circuit diagram is shown in Fig. 2.1.

|
Notice that the diagram is read from left to right. This means that if two consecutive
gates are implemented, say first and then , the equation reads:
| (2.6) |
The circuit diagram will have the boxes in the reverse order from the equation, i.e. on the left and on the right (refer to Fig. 2.2 below). While this is somewhat confusing, it is important to remember convention; circuit diagrams will become increasingly important as the number of operations grows larger.

|
Examples of Important Qubit Gates
There are, of course, an infinite number of possible unitary transformations that we could implement on a single qubit since the set of unitary transformations can be parameterized by three parameters. However, a single gate will contain a single unitary transformation, which means that all three parameters are fixed. There are several such transformations that are used repeatedly. For this reason, they are listed here along with their actions on a generic state . Note that one could also completely define the transformation by its action on a complete set of basis states.
The following is called an “x” gate, or a bit-flip,
| (2.7) |
Its action on a state is to exchange the basis states,
| (2.8) |
for this reason it is also sometimes called a NOT gate. However, this term will be avoided because a general NOT gate does not exist for all quantum states. (It does work for all qubit states, but this is a special case.)
The next gate is called a phase gate or a “z” gate. It is also sometimes called a phase-flip, and is given by
| (2.9) |
The action of this gate is to introduce a sign change on the state which can be seen through
| (2.10) |
The term phase gate is also used for the more general transformation
| (2.11) |
For this reason, the z-gate will either be called a “z-gate” or a phase-flip gate.
Another gate closely related to these, is the “y” gate. This gate is
| (2.12) |
The action of this gate on a state is
| (2.13) |
From this last expression, it is clear that, up to a factor of , this gate is the same as acting on a state with both and gates. However, the order matters, and it should be noted that
whereas
The fact that the order matters should not be a surprise to anyone since matrices in general do not commute. However, such a condition arises so often in quantum mechanics that the difference between these two is given an expression and a name. The difference between the two is called the commutator and is denoted with a . That is, for any two matrices, and , the commutator is defined to be
| (2.14) |
For the two gates and ,
| (2.15) |
A very important gate which is used in many quantum information processing protocols, including quantum algorithms, is called the Hadamard gate,
| (2.16) |
In this case, its helpful to look at what this gate does to the two basis states:
| (2.17) |
So the Hadamard gate will take either one of the basis states and produce an equal superposition of the two basis states; this is the reason it is so-often used in quantum information processing tasks. On a generic state, (e.g., Eq.(2.1))
| (2.18) |
The Pauli Matrices
The three matrices Eq.(2.7), Eq.(2.12), and Eq.(2.9) are called the Pauli matrices. They are also sometimes denoted , and , or , and respectively. They are ubiquitous in quantum computing and quantum information processing. This is because they, along with the identity matrix, form a basis for the set of Hermitian matrices and can be used to describe all unitary transformations as well. We will return to the latter point in the next chapter.
| Pauli Matrix | Notation 1 | Notation 2 | Notation 3 | Action |
To show that they form a basis for Hermitian matrices, note that any such matrix can be written in the form
| (2.19) |
Since and are arbitrary, and are arbitrary too. This matrix can be written as
| (2.20) |
where is the "dot product" between and .
An important and useful relationship between these is the following (which shows why the latter notation above is so useful)
| (2.21) |
where are numbers from the set and the definitions for and are given in Eqs. (C.17) and (C.8) respectively. The three matrices are traceless Hermitian matrices and they can be seen to be orthogonal using the so-called Hilbert-Schmidt inner product, which is defined, for matrices and , as
| (2.22) |
The orthogonality for the set is then summarized as
| (2.23) |
This property is contained in Eq. (2.21). This one equation also contains all of the commutators. Subtracting the equation with the product reversed,
| (2.24) |
but and . This can now be simplified,
| (2.25) |
States of Many Qubits
Let us now consider the states of several (or many) qubits. For one qubit, there are two possible basis states, say and . If there are two qubits, each with these basis states, basis states for the two together are found by using the tensor product (see Appendix C.7, Tensor Products). The set of basis states obtained in this way is
This set is more often written in short-hand notation as (again see Appendix C.7, Tensor Products for details and examples)
| (2.26) |
which can also be expressed as
| (2.27) |
The extension to three qubits is straight-forward,
| (2.28) |
Those familiar with binary will recognize these as the numbers zero through seven. Thus we consider this an ordered basis. Thus, they can also be acceptably presented as
| (2.29) |
The ordering of the products is important because each spot corresponds to a physical particle or physical system. When some confusion may arise, we may also label the ket with a subscript to denote the particle or position. For example, two different people, Alice and Bob, can be used to represent distant parties that may share some information or wish to communicate. In this case, the state belonging to Alice can be denoted . Or if she is referred to as party 1 or particle 1, .
The most general 2-qubit state is written as
| (2.30) |
The normalization condition is The generalization to an arbitrary number of qubits, say , is also rather straight-forward and can be written as
Quantum Gates for Many Qubits
Just as the case for one single qubit, the most general closed-system transformation of a state of many qubits is a unitary transformation. Being able to make an arbitrary unitary transformation on many qubits is an important task. If an arbitrary unitary transformation on a set of qubits can be made, then any quantum gate can be implemented. If this ability to implement any arbitrary quantum gate can be accomplished using a particular set of quantum gates, that set is said to be a universal set of gates or that the condition of universality has been met by this set. It turns out that there is a theorem which provides one way for identifying a universal set of gates.
Theorem:
The ability to implement a special class of two-qubit gates, called entangling gates[1], between any two qubits, plus the ability to implement all single-qubit unitary transformations, will enable universal quantum computing.
It turns out that one doesn’t need to be able to perform an entangling gate between distant qubits; nearest-neighbor interactions are sufficient. We can transfer the state of a qubit to a qubit that is next to the one we would like it to interact with, then perform the entangling gate between the two and then transfer back.
This is an important and often used theorem which will be the main focus of the next few sections. A particular class of two-qubit gates which can be used to entangle qubits will be discussed along with circuit diagrams for many qubits.
Controlled Operations
One of the special types of two-qubit gates that may be called "entangling" is the following "controlled operation." A controlled operation is one that is conditioned on the state of another part of the system, usually a qubit. The most cited example is the CNOT (controlled NOT) gate, which flips one (target) bit if another qubit (called the "control") is in the state ; thus it is controlled NOT operation for qubits. This gate is used often enough to warrant detailed discussion here.
Consider the following matrix operation on two qubits:
| (2.31) |
Under this transformation, the following changes occur:
| (2.32) |
This transformation is called the CNOT, or controlled NOT, since the second bit is flipped if the first is in the state and otherwise left alone. The subscripts on the CNOT gates are necessary since the qubit which is to serve as the control and which is to serve as the target. This is the purpose. The circuit diagram for this transformation corresponds to the following representation of the gate. Let and be zero or one. The CNOT is then given by
| (2.33) |
In binary, of course , , and . The circuit diagram is given in Fig. 2.3 below. The first qubit at the top of the diagam, , is called the control bit while the one below, , is called the target bit.
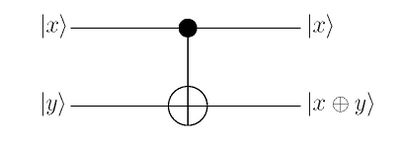
|
Figure 2.3: Circuit diagram for a CNOT gate.
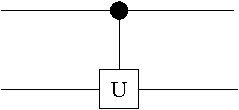
One can immediately generalize the operation of the CNOT to a controlled-U gate. This is a gate, shown in Fig. 2.4, which implements a unitary transformation on the second qubit, if the state of the first is . The matrix transformation is given by
| (2.34) |
where the matrix
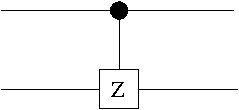
For example the controlled-phase gate is given in Fig. 2.5.
Many-qubit Circuits
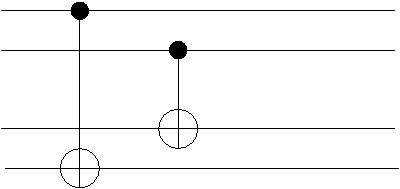
Many qubit circuits are a straight-forward generalization of the single quibit circuit diagrams. For example, Fig. 2.6 shows the implementation of CNOT and CNOT in the same diagram. The crossing of lines is not confusing since there is a target and control which are clearly distinguished in each case.
It is quite interesting however, that as the diagrams become more complicated, the possibility arises that one may change between equivalent forms of a circuit that, in the end,
implements the same multiple-qubit unitary. For example, noting that , the two circuits in Fig. 2.7 implement the same two-qubit unitary transformation. This enables the simplication of some quite complicated circuits.
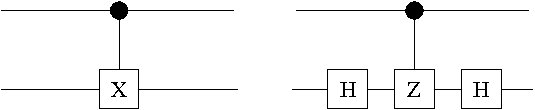
Figure 2.7: Two circuits which are equivalent since they implement the same two-qubit
unitary transformation.
Measurement
Measurement in quantum mechanics is quite different from that of classical mechanics. In classical mechanics (and classical computing), one assumes that a measurement can be made at will without disturbing or changing the state of the physical system. In quantum mechanics, this assumption cannot be made. This is important for a variety of reasons that will hopefully become clear later.
Born Rule
The standard prescription, or rule, for quantum measurement is sometimes called the Born rule. This is very well described in Mermin's book [1]. Here, we provide some examples and a brief description of the rule and how to use it. It should be stated, however, that the rule does not actually describe what physically takes place during a measurement. Everything is quantum mechanical and thus a measurement should properly be described by an interaction between two quantum mechanical objects. The Born rule is a good approximation to this for a variety of physical systems. It is also much simpler than a fully quantum mechanical treatment. Thus we use this throughout our discussions unless otherwise stated.
As an example, consider the quantum state in a superposition of and of the form
| (2.35) |
with . If the state is measured in the computational basis (the basis), the result will be with probability and with probability . As always, it is important to note that this state is not in one of the computational basis states, but is in a superposition of the two. Immediately after the measurement, the system, or particle, will be in the state that was found when the state was measured. For example, if the state was obtained, which it will be with probability , then the state immediately after the measurement will be . If the state was obtained, which it will be with probability , then the state immediately after the measurement will be .
Note that one cannot say that the system was in the state with some probability. The system was in the state . When it is measured, we obtain the result with some probability.
This can be easily shown by acting on the state with a Hadamard transformation,
| (2.36) |
This state, produced from a unitary transformation of , has probability of being in the state and probability of being in the state . If it were in one or the other, then acting on the state with a Hadamard transformation would give some probability of it being in and some probability of being in . (This argument is so simple and pointed that it was taken almost word-for-word from Mermin's book [1], page 27.)
A measurement in the computational basis is said to project this state into either the state or the state with probabilities and respectively. To understand this as a projection, consider the following way in which the -component of the state is found. The state is projected onto the the state mathematically by taking the inner product (see Section C.4, More Dirac Notation) of and
| (2.37) |
Notice that this is a complex number and that its complex conjugate can be expressed as
| (2.38) |
Therefore the probability can be expressed as
| (2.39) |
Now consider a multiple-qubit system with state
| (2.40) |
The result of a measurement is a projection and the state is projected onto the basis state with probability ---the same properties are true of this more general system.
To summarize, if a measurement is made on the system , the result is obtained with probability . Assuming that results from the measurement, the state of the system has been projected into the state . Therefore, the state of the system immediately after the measurement is .
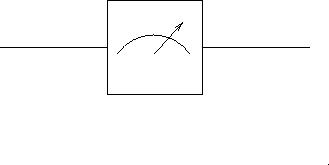
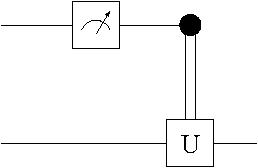
A circuit diagram with a measurement represented by a box with an arrow is given in Figure 2.8.
An alternative is to put an "M" inside the box. This is shown in Fig. 2.9.
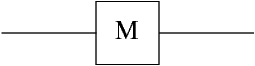
Figure 2.9: An alternative circuit diagram for a measurement.
As an example, the measurement result can be used for input for another state. The unitary transform in Figure 2.10 is one that depends upon the outcome of the measurement. Notice that the information input, since it is classical, is represented by a double line.
Projection Operators
Projection operators are used quite often and the description of measurement in the previous section is a good example of how they are used. One may ask, what is a projector? In ordinary three-dimensional space, a vector is written as and the part of the vector can be obtained by
| (2.40) |
This is the part of the vector lying along the x axis. Notice that if the projection is performed again, the same result is obtained
| (2.41) |
This is (the) characteristic of projection operations. When one is performed twice, the second result is the same as the first.
This can be extended to the complex vectors in quantum mechanics. The outer product (see Appendix C.2.4, Outer Product) is a projector. For example, is a projector and can be written in matrix form as
| (2.42) |
Acting with this on gives
| (2.43) |
Acting again produces
| (2.44) |
This is due to the fact that
| (2.45) |
In fact, this property essentially defines a projection. A projection is a linear, hermitian transformation such that . Much of our intuition about geometric projections in three-dimensions carries to the more abstract cases. One important example is that the sum over a complete set of orthonormal projections is the identity. The generalization to arbitrary dimensions, where is any basis vector in that space, is immediate. In this case the identity, expressed as a sum over a complete set of orthonormal projectors, is
| (2.46) |
Phase in/Phase out
The probability of finding the system in the state , where or , is
| (2.47) |
Note that and both appear in this expression. So if were substituted into the expression for , then the expression is unchanged,
| (2.48) |
Therefore when changes by a phase, there is no effect on this probability. This is why it is often said that
| (2.49) |
is equivalent to
| (2.50) |
However, there are times when a phase can make a difference. In those cases it is really a relative phase between two states that makes the difference. Examples of this will be seen in later sections.
Exercises
Continue to Chapter 3 - Physics of Quantum Information
Footnotes
- ↑ An entangling gate is one that has the ability to entangle two qubits. At this point, we have not defined entanglement. This will be done in Chapter 4. For now, we can just take this to mean a non-trivial two-qubit interaction, or special class of non-trivial two-quit gates, and defer the slightly more technical discussion of what this means until later.































![{\displaystyle [\cdot ,\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28dd4c22d60192519c1c12cf645b040f368db9e9)


![{\displaystyle [A,B]=AB-BA.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc13a2c0ff58c7ee510c2d7d37857c53d871cb8)
![{\displaystyle [X,Z]=-2iY.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/831123cb123376dead54c1d6e9ad9fec37276f7a)



![{\displaystyle H\left\vert {\psi }\right\rangle ={\frac {1}{\sqrt {2}}}[(\alpha _{0}+\alpha _{1})\left\vert {0}\right\rangle +(\alpha _{0}-\alpha _{1})\left\vert {1}\right\rangle ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3ae63d1ddad79fffbcf74effe1131d1f5c1519b)






































![{\displaystyle [\sigma _{i},\sigma _{j}]=(\mathbb {I} \delta _{ij}+i\epsilon _{ijk}\sigma _{k})-(\mathbb {I} \delta _{ji}+i\epsilon _{jik}\sigma _{k}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0dd60a99c48a0baf2c62534b00e1abecfad340)


![{\displaystyle [\sigma _{i},\sigma _{j}]=2i\epsilon _{ijk}\sigma _{k}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d715ceae7e9ac56fa110e58239bc5924531b3531)