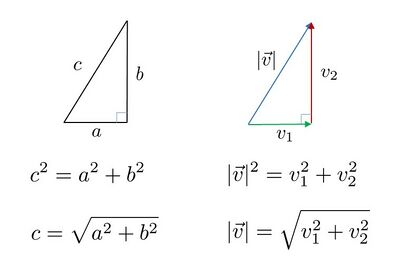Vectors: A beginner's guide

Here we introduce vectors and the notation that we use for vectors. We then give some facts about real vectors before discussing the complex vectors used in quantum mechanics.

Vectors: Defining and Representing

You may have heard of the definition of a vector as a quantity with both magnitude and direction. While this is true and often used in science classes, our purpose is different. So we will simply define a vector as a set of numbers that is written in an row or a column. When the vector is written as a row of numbers, it is called a row vector and when it is written as a set of numbers in a column, it is called a column vector. As we will see, these two can have the same set of numbers, but each can be used in a slightly different way.

Note that a vector with two entries, or two numbers, is called a two-dimensional vector. One with three entries is called a three-dimensional vector, etc.

Examples

This is an example of a two-dimensional row vector ${\vec {s}}=(1,6).$

This is an example of a two-dimensional column vector ${\vec {u}}=\left({\begin{array}{c}7\\2\end{array}}\right).$

This is an example of a three-dimensional row vector ${\vec {v}}=(2,4,3).$

This is an example of a three-dimensional column vector ${\vec {w}}=\left({\begin{array}{c}1\\5\\4\end{array}}\right).$

Real Vectors

(If you are not familiar with vectors, you can skip this subsection.)

If you are familiar with vectors, the simple definition of a vector --- an object that has magnitude and direction --- is helpful to keep in mind even when dealing with complex vectors (vectors with complex, i.e., imaginary numbers as entries) as we will here. However, this is not necessary and we will see how to perform all of the operations that we need just using arrays of numbers that we call vectors. In three dimensional space, a vector is often written as

${\vec {v}}=v_{x}{\hat {x}}+v_{y}{\hat {y}}+v_{z}{\hat {z}},$

where the hat (${\hat {\cdot }}\,\!$) denotes a unit vector and the components $v_{i}\,\!$, $i=x,y,z\,\!$ are just numbers. The unit vectors are also known as basis vectors. This is because any vector in real three-dimensional space can be written in terms of these unit/basis vectors. In this vector, one can associate a point where the coordinate of the point is $(x,y,z)$. That is, a point a distance $x$ from the origin along the $x$-axis, a distance $y$ from the origin along the $y$-axis, and a distance $z$ from the origin along the $z$-axis. In some sense, unit vectors are the basic components of any vector. Other basis vectors could be used. But this will be discussed elsewhere.

Vector Operations

To illustrate vector operations, let

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right),{\mbox{ and }}{\vec {w}}=\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right).$

Also, let

${\vec {s}}=\left(s_{1},s_{2}\right),{\mbox{ and }}{\vec {u}}=\left(u_{1},u_{2}\right).$

Vector Addition

Vectors can be added. To do this, each element of one vector is added to the corresponding element of the other vector. In general, for a row vector, they add as

${\vec {v}}+{\vec {w}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)+\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right)=\left({\begin{array}{c}v_{1}+w_{1}\\v_{2}+w_{2}\end{array}}\right).$

The addition of row vectors is similar. They are added component by component. Then

${\vec {s}}+{\vec {u}}=\left(s_{1},s_{2}\right)+\left(u_{1},u_{2}\right)=\left(s_{1}+u_{1},s_{2}+u_{2}\right).$

Since the way vectors are added is component to corresponding component, it is important to note that you can only add vectors if they are the same type. (No adding "apples and oranges" so to speak.) So you can add two vectors that are both column vectors and have three entries. You can't add a column vector to a row vector and you can't add a vector with two components to a vector with three components.

Example

Adding two vectors ${\vec {v}}_{1}\,\!$ and ${\vec {w}}_{1}\,\!$ with

${\vec {v}}_{1}=\left({\begin{array}{c}1\\5\end{array}}\right),\;\;{\vec {w}}_{1}=\left({\begin{array}{c}4\\2\end{array}}\right),\,\!$

we get

${\vec {v}}_{1}+{\vec {w}}_{1}=\left({\begin{array}{c}1\\5\end{array}}\right)+\left({\begin{array}{c}4\\2\end{array}}\right)=\left({\begin{array}{c}5\\7\end{array}}\right).\,\!$

Multiplication by a Number

When a vector is multiplied by a number, each component is multiplied by that same number. For example, suppose

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

Then

$a{\vec {v}}=a\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)=\left({\begin{array}{c}av_{1}\\av_{2}\end{array}}\right).$

Length or Magnitude of a Vector

Consider the vector

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

We can calculate the length of a vector the same way that one calculates the hypotenuse of a right triangle. The magnitude is the square root of the sum of the squares of the entries. For example,

$|{\vec {v}}|={\sqrt {(v_{1})^{2}+(v_{1})^{2}}}.$

Figure V.1: The magnitude of a vector in terms of its entries.

Vectors of Length One, Unit Vectors

Vectors of length, or magnitude $=1$ are quite useful. These are also called "unit vectors". As we will see, they are used as "basis vectors" and also for quantum states. If a vector does not have length one, but it should have, then we can "normalize" it by dividing by the magnitude. When this is done, the vector of length one is often denoted with a "hat" ${\hat {v}}$ instead of the arrow ${\vec {v}}$. So

${\hat {v}}={\frac {1}{|{\vec {v}}|}}{\vec {v}}={\frac {1}{|{\vec {v}}|}}\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

The magnitude of this vector is

$|{\vec {v}}|={\sqrt {v_{1}^{2}+v_{2}^{2}}}.$

Then to see that the vector ${\vec {v}}$ is normalized,

${\begin{aligned}|{\hat {v}}|&={\sqrt {\frac {\vec {v}}{|{\vec {v}}|}}}\\&\\&={\sqrt {\left({\frac {v_{1}}{|{\vec {v}}|}}\right)^{2}+\left({\frac {v_{2}}{|{\vec {v}}|}}\right)^{2}}}\\&\\&={\frac {1}{|{\vec {v}}|}}{\sqrt {(v_{1})^{2}+(v_{2})^{2}}}=1.\end{aligned}}$

Notice that, in general, if the vector is multiplied by a number $a$ that is positive, then the magnitude of the vector is

$|a{\vec {v}}|={\sqrt {(av_{1})^{2}+(av_{1})^{2}}}={\sqrt {a^{2}(v_{1}^{2}+v_{2}^{2})}}=|a||{\vec {v}}|.$

So multiplying a vector by a number just changes the length, or magnitude, of the vector is $a$ is positive. If $a$ is negative, it changes the directions of the components and therefore of the vector itself and also changes the magnitude.

Dot Products or Inner Products

The inner product, or dot product, for two real two-dimensional vectors,

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right),{\mbox{ and }}{\vec {w}}=\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right)$

or

${\vec {s}}=\left(s_{1},s_{2}\right),{\mbox{ and }}{\vec {u}}=\left(u_{1},u_{2}\right).$

can be computed as follows:

${\vec {v}}\cdot {\vec {w}}=v_{1}w_{1}+v_{2}w_{2},{\mbox{ and }}{\vec {s}}\cdot {\vec {u}}=s_{1}u_{1}+s_{2}u_{2}.$

For the inner product of ${\vec {v}}\,\!$ with itself, we get the square of the magnitude of ${\vec {v}}\,\!$, denoted $|{\vec {v}}|^{2}\,\!$:

$|{\vec {v}}|^{2}={\vec {v}}\cdot {\vec {v}}=v_{1}v_{1}+v_{2}v_{2}=v_{1}^{2}+v_{2}^{2}.$

If we want a unit vector in the direction of ${\vec {v}}\,\!$, we can simply divide it by its magnitude:

${\hat {v}}={\frac {\vec {v}}{|{\vec {v}}|}}.$

Now, of course, ${\hat {v}}\cdot {\hat {v}}=1\,\!$, which can easily be checked.

There are several ways to represent a vector. The ones we will use most often are column and row vector notations. So, for example, we could write the vector above as

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

In this case, our unit vectors are represented by the following:

${\hat {e}}_{1}=\left({\begin{array}{c}1\\0\end{array}}\right),\;\;{\hat {e}}_{2}=\left({\begin{array}{c}0\\1\end{array}}\right).\,\!$

$e_{1}\,\!$ and $e_{2}\,\!$ are called basis vectors. Notice they are unit vectors.

Any vector can be rewritten in terms of these basis vectors. For example,

${\vec {v}}=v_{1}{\hat {e}}_{1}+v_{2}{\hat {e}}_{2}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

We next turn to the subject of complex vectors and the relevant notation. We will see how to compute the inner product later, since some other definitions are required.

Complex Vectors

A complex vector is one that has complex numbers for entries. For complex vectors in quantum mechanics, Dirac notation is used most often. This notation uses a $\left\vert \cdot \right\rangle \,\!$, called a ket, for a vector. So our vector ${\vec {v}}\,\!$ would be

$\left\vert v\right\rangle =\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

For qubits, i.e. two-state quantum systems, complex vectors will often be used:

	${\begin{aligned}\left\vert \psi \right\rangle &=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\alpha \left\vert 0\right\rangle +\beta \left\vert 1\right\rangle ,\end{aligned}}$	(V.1)

where

	$\left\vert 0\right\rangle =\left({\begin{array}{c}1\\0\end{array}}\right),\;\;{\mbox{and}}\;\;\left\vert 1\right\rangle =\left({\begin{array}{c}0\\1\end{array}}\right)$	(V.2)

are the basis vectors. The two numbers $\alpha \,\!$ and $\beta \,\!$ are complex numbers, so the vector is said to be a complex vector. Recall from Chapter 1 that quantum states are represented by complex vectors, such as the quantum particle being in one of two different wells.

The Complex Conjugate of a Vector

To take the complex conjugate of a vector, each element of the vector has to be complex conjugated. So,

	${\begin{aligned}(\left\vert \psi \right\rangle )^{*}&=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{*}\\&=\left({\begin{array}{c}\alpha ^{*}\\\beta ^{*}\end{array}}\right)\\&=\alpha ^{*}\left\vert 0\right\rangle +\beta ^{*}\left\vert 1\right\rangle .\end{aligned}}$	(V.3)

The Transpose of a Vector

Let us reconsider the vector from above,

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

To transpose this vector, the vector will be turned into a row vector. It is the almost the same vector, just made into a row vector. The transpose is denoted with a superscript $T$:

${\begin{aligned}{\vec {v}}^{T}&=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)^{T}\\&=\left({\begin{array}{cc}v_{1},&v_{2}\end{array}}\right).\end{aligned}}$

The Hermitian Conjugate, or "Dagger", of a Vector

The "dagger" of a vector, which is also called the hermitian conjugate, is the transpose and complex conjugate. This is denoted by a "dagger" superscript $^{\dagger }$

${\begin{aligned}({\vec {v}}^{*})^{T}&=\left({\begin{array}{c}v_{1}^{*}\\v_{2}^{*}\end{array}}\right)^{T}\\&=\left({\begin{array}{cc}v_{1}^{*},&v_{2}^{*}\end{array}}\right).\end{aligned}}$

In the case of complex vectors, the following notation is used:

	${\begin{aligned}(\left\vert \psi \right\rangle )^{\dagger }&=\left\langle \psi \right\vert \\&=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{\dagger }\\&=\left({\begin{array}{cc}\alpha ^{*},&\beta ^{*}\end{array}}\right).\end{aligned}}$	(V.4)

Complex Inner Product

To calculate the inner product of two complex, two-dimensional vectors, the complex conjugate of one is multiplied, term by term with the second. So if vectors ${\vec {v}}$ and ${\vec {w}}$ are complex vectors, the inner product, or dot product, is calculated by

${\vec {v}}\cdot {\vec {w}}={\vec {v}}^{\dagger }{\vec {w}}=v_{1}^{*}w_{1}+v_{2}^{*}w_{2}.$

This enables the inner product between two vectors to be written as

$(\langle {v}|)(|{w}\rangle )={\vec {v}}^{\dagger }{\vec {w}}=v_{1}^{*}w_{1}+v_{2}^{*}w_{2}.$

and the inner product of a vector with itself

$\langle \psi |\psi \rangle =\alpha ^{*}\alpha +\beta ^{*}\beta .$

Basis Vectors

Basis vectors are vectors that can be used to write any other vector. For example, any two-dimensional vector such as

${\begin{aligned}\left\vert \psi \right\rangle &=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\alpha \left\vert 0\right\rangle +\beta \left\vert 1\right\rangle ,\end{aligned}},$

can be written in terms of the two basis vectors $\left|0\right\rangle$ and $\left|1\right\rangle$. That is because Failed to parse (syntax error): {\displaystyle \begin{align} \left\vert \psi \right\rangle &= \left(\begin{array}{c} \alpha \\ \beta \end{array}\right) \\ &=\alpha \left(\begin{array}{c} 1 \\ 0 \end{array}\right) + \beta\left(\begin{array}{c} 0 \\ 1 \end{array}\right),\end{align} \\ &=\alpha \left\vert 0\right\rangle + \beta\left\vert 1\right\rangle,\end{align}, }

Exercises

To illustrate vector operations, let

$\left|r\right\rangle =\left({\begin{array}{c}1\\i\end{array}}\right),\;\;\left|s\right\rangle =\left({\begin{array}{c}1+i\\3\end{array}}\right),{\mbox{ and }}\left|t\right\rangle =\left({\begin{array}{c}-2i\\2\end{array}}\right).$

1. Vectors
1. Calculate the complex conjugate of $\left|r\right\rangle ,\;\left|s\right\rangle ,\;{\mbox{and}}\left|t\right\rangle .$
2. Calculate the magnitudes of all three vectors.
3. Normalize $\left|r\right\rangle ,\;\left|s\right\rangle ,{\mbox{ and }}\left|t\right\rangle$. Confirm that they are now unit vectors.
4. Calculate the Hermitian conjugate (dagger) of all three vectors.
2. Dirac Notation (bras, kets, and brackets)
1. Calculate the inner product $\left\langle s|t\right\rangle$, between $\left|s\right\rangle ,\;{\mbox{and}}\left|t\right\rangle .$
2. Calculate the inner products among all three vectors normalized versions of the vectors. Is there any pair that is orthogonal?
3. What can you say about the magnitude of the inner products in relation to the magnitudes of the individual vectors?
4. Find the inner product between $\left|0\right\rangle ,{\mbox{ and }}\left|1\right\rangle$ from Eq.(V.2).

Copyright

© Copyright 2022 BKR Collaboration