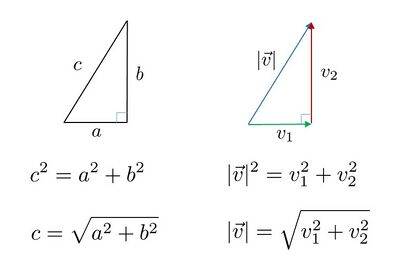Testing

---EPR Paradox---

Before diving into entanglement in the context of quantum computing and information, it would be prudent to discuss the now-famous EPR paradox. It was first proposed in a paper by Einstein, Polosky, and Rosen in 1935. The original paper does include a fairly simple mathematical explanation of the paradox---it is, however, not really necessary as the thought experiment is quite easily understood conceptually with (mostly) words. A slightly simplified version of the experiment will be given here.

Suppose a neutral pi meson, which has no spin, is at rest. It then decays into an electron and a positron, necessarily going in opposite directions. The wave function can now be written as

	$\left\vert \Psi _{-}\right\rangle ={\frac {1}{\sqrt {2}}}(\left\vert \uparrow \downarrow \right\rangle -\left\vert \downarrow \uparrow \right\rangle ).$	(4.1)

As can be seen, we now have a system of two particles that have a correlated spin---one being up and the other being down---with an equal probability for each configuration being the outcome of a measurement. The system is said to be entangled, as a measurement on one will guarantee that the other particle is in the correlated state. In other words, it cannot be written as $\left\vert \psi _{1}\right\rangle \left\vert \psi _{2}\right\rangle$.

Now what is the significance here? It all depends on what interpretation of quantum mechanics is being used. The orthodox position says that the wave function is the complete representation of the system. When the measurement occurs, the wave function collapses, changing the system.

But, in the context of EPR, how can this be? Imagine the entangled electron-positron pair are at opposite ends of the galaxy when one of them is measured. The conservation of angular momentum says that the other particle all of the way on the other side of the galaxy must instantly be the opposite spin as the measured particle. EPR argued that this is a violation of locality, which says an effect cannot travel faster than the speed of light. If the very action of measurement on one particle is what caused the other particle to realize the opposite spin, then locality has been violated. Therefore, the measurement could not have caused the collapse of the wave function.

EPR concluded that this proves that quantum mechanics is incomplete---that the wave function is missing some information. There was no "spooky-action-at-a-distance," there must be some underlying property that is absent from the wave function. Einstein rejected the notion that a measurement caused this quasi-mystical collapse of the wave function---the particles do not care if they are being watched or not.

---Bell's Theorem---

The peculiarities of the EPR paradox were convincing enough to drive many to examine possible "hidden variable theories." The basic idea is that there exists a quantity, often denoted by $\lambda \,\!$, that must be included in the wave function to completely describe the system. J.S. Bell very elegantly showed in 1964 that this is not the case, using the very thought experiment (although slightly modified) that EPR proposed.

Suppose we have another pion at rest about to decay with detectors oriented equidistant and on opposite sides, ready to measure the spin of the electron and positron. Further suppose that, unlike the previous scenario, these detectors can be rotated in order to detect the spin in the direction of unit vectors ${\vec {a}}\,\!$ and ${\vec {b}}$ for the electron and positron respectively.

When the electron and positron pair strikes the detectors, a spin up ($-1$) or spin down ($-1\,\!$) is registered. The product of the results is then examined. If they are oriented parallel, where ${\vec {a}}={\vec {b}}\,\!$, then the result will be -1. If anti-parallel, the result is then +1. The averages are, obviously,

	${\begin{aligned}P({\vec {a}},{\vec {a}})&=-1,\\P({\vec {a}},-{\vec {a}})&=+1.\end{aligned}}\,\!$	(4.2)

Quantum mechanics tells us that for arbitrary vectors,

	$P({\vec {a}},{\vec {b}})=-{\vec {a}}\cdot {\vec {b}}.\,\!$	(4.3)

We can now introduce the hidden variable, $\lambda$. This can represent any possible amount of variables that complete the description of the system and allow for locality. We then define some functions, $A({\vec {a}},\lambda )$ and $B({\vec {b}},\lambda ),$ that will give the results for the measurement (either +1 or -1) for the electron and positron respectively.

The locality assumption tells us that the orientation of one detector will not affect the outcome of the measurement of the other detector; one can imagine a scenario where the orientation is chosen at a time too late for any information to be transfered slower than light. It must also be true that, when the detectors are parallel, the results must be

	$A({\vec {a}},\lambda )=-B({\vec {a}},\lambda )\,\!$	(4.4)

due to the conservation of angular momentum. Let us also define a probability density, $\rho (\lambda ),\,\!$ for the hidden variable. Since we know nothing of $\lambda \,\!$, this can be anything as long as it is nonnegative and normalizable ($\int \rho (\lambda )d(\lambda )=1\,\!$). We can now look at the product of the measurements,

	$P({\vec {a}},{\vec {b}})=\int \rho (\lambda )A({\vec {a}},\lambda )B({\vec {b}},\lambda )d\lambda .\,\!$	(4.5)

We know from Eq.(4.4) that this can be rewritten:

	$P({\vec {a}},{\vec {b}})=-\int \rho (\lambda )A({\vec {a}},\lambda )A({\vec {b}},\lambda )d\lambda .\,\!$	(4.6)

Now for the clever part. Introducing another unit vector, ${\vec {c}}$, and noting that $[A({\vec {b}},\lambda )]^{2}=1,\,\!$

	${\begin{aligned}P({\vec {a}},{\vec {b}})-P({\vec {a}},{\vec {c}})&=-\int \rho (\lambda )[A({\vec {a}},\lambda )A({\vec {b}},\lambda )-A({\vec {a}},\lambda )A({\vec {c}},\lambda )]d\lambda \\&=-\int \rho (\lambda )[1-A({\vec {b}},\lambda )A({\vec {c}},\lambda )]A({\vec {a}},\lambda )A({\vec {b}},\lambda )d\lambda \end{aligned}}\,\!$	(4.7)

Recognizing some inequalities,

	${\begin{aligned}-1\leq A({\vec {a}},\lambda )A({\vec {b}},\lambda )\leq 1,\\\rho (\lambda )[1-A({\vec {b}},\lambda )A({\vec {c}},\lambda )]\geq 0,\end{aligned}}\,\!$	(4.8)

we get to a remarkable result,

	${\begin{aligned}|P({\vec {a}},{\vec {b}})-P({\vec {a}},{\vec {c}})|&\leq \int \rho (\lambda )[1-A({\vec {b}},\lambda )A({\vec {c}},\lambda )]d\lambda \\&\leq 1+P({\vec {b}},{\vec {c}}).\end{aligned}}\,\!$	(4.9)

The last form is known as the Bell inequality. This inequality is true for any local hidden variable theory.

What does this mean? Let us define ${\vec {a}}\,\!$ and ${\vec {b}}\,\!$ to be orthogonal and ${\vec {c}}\,\!$ to make a $45^{\circ }\,\!$ angle with both of them. Using quantum mechanics (Equation(4.3)),

${\begin{aligned}P({\vec {a}},{\vec {b}})=0\\P({\vec {a}},{\vec {c}})=P({\vec {b}},{\vec {c}})=-{\frac {1}{\sqrt {2}}}.\end{aligned}}\,\!$

Inserting the values into the Bell inequality (Equation (4.9)),

${\begin{aligned}\left|-{\frac {1}{\sqrt {2}}}\right|&\leq 1+\left(-{\frac {1}{\sqrt {2}}}\right)\\{\frac {1}{\sqrt {2}}}&\leq {\frac {{\sqrt {2}}-1}{\sqrt {2}}}\\1&\leq {\sqrt {2}}-1\end{aligned}}\,\!$

Since ${\sqrt {2}}-1\approx .41,\,\!$ the inequality is violated!

This means that quantum mechanics is incompatible with any local hidden variable theory. The EPR paradox had stronger implications than the authors realized; if local realism is held, then quantum mechanics is incorrect. This has been repeatedly disproved experimentally. Thus no local hidden variable theory can resolve the "spooky-action-at-a-distance."

Here we introduce vectors and the notation that we use for vectors. We then give some facts about real vectors before discussing the complex vectors used in quantum mechanics.

Vectors: Defining and Representing

You may have heard of the definition of a vector as a quantity with both magnitude and direction. While this is true and often used in science classes, our purpose is different. So we will simply define a vector as a set of numbers that is written in an row or a column. When the vector is written as a row of numbers, it is called a row vector and when it is written as a set of numbers in a column, it is called a column vector. As we will see, these two can have the same set of numbers, but each can be used in a slightly different way.

Note that a vector with two entries, or two numbers, is called a two-dimensional vector. One with three entries is called a three-dimensional vector, etc.

Examples

This is an example of a two-dimensional row vector ${\vec {s}}=(1,6).$

This is an example of a two-dimensional column vector ${\vec {u}}=\left({\begin{array}{c}7\\2\end{array}}\right).$

This is an example of a three-dimensional row vector ${\vec {v}}=(2,4,3).$

This is an example of a three-dimensional column vector ${\vec {w}}=\left({\begin{array}{c}1\\5\\4\end{array}}\right).$

Real Vectors

(If you are not familiar with vectors, you can skip this subsection.)

If you are familiar with vectors, the simple definition of a vector --- an object that has magnitude and direction --- is helpful to keep in mind even when dealing with complex vectors (vectors with complex, i.e., imaginary numbers as entries) as we will here. However, this is not necessary and we will see how to perform all of the operations that we need just using arrays of numbers that we call vectors. In three dimensional space, a vector is often written as

${\vec {v}}=v_{x}{\hat {x}}+v_{y}{\hat {y}}+v_{z}{\hat {z}},$

where the hat (${\hat {\cdot }}\,\!$) denotes a unit vector and the components $v_{i}\,\!$, $i=x,y,z\,\!$ are just numbers. The unit vectors are also known as basis vectors. This is because any vector in real three-dimensional space can be written in terms of these unit/basis vectors. In this vector, one can associate a point where the coordinate of the point is $(x,y,z)$. That is, a point a distance $x$ from the origin along the $x$-axis, a distance $y$ from the origin along the $y$-axis, and a distance $z$ from the origin along the $z$-axis. In some sense, unit vectors are the basic components of any vector. Other basis vectors could be used. But this will be discussed elsewhere.

Vector Operations

To illustrate vector operations, let

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right),{\mbox{ and }}{\vec {w}}=\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right).$

Also, let

${\vec {s}}=\left(s_{1},s_{2}\right),{\mbox{ and }}{\vec {u}}=\left(u_{1},u_{2}\right).$

Vector Addition

Vectors can be added. To do this, each element of one vector is added to the corresponding element of the other vector. In general, for a row vector, they add as

${\vec {v}}+{\vec {w}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)+\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right)=\left({\begin{array}{c}v_{1}+w_{1}\\v_{2}+w_{2}\end{array}}\right).$

The addition of row vectors is similar. They are added component by component. Then

${\vec {s}}+{\vec {u}}=\left(s_{1},s_{2}\right)+\left(u_{1},u_{2}\right)=\left(s_{1}+u_{1},s_{2}+u_{2}\right).$

Since the way vectors are added is component to corresponding component, it is important to note that you can only add vectors if they are the same type. (No adding "apples and oranges" so to speak.) So you can add two vectors that are both column vectors and have three entries. You can't add a column vector to a row vector and you can't add a vector with two components to a vector with three components.

Example

Adding two vectors ${\vec {v}}_{1}\,\!$ and ${\vec {w}}_{1}\,\!$ with

${\vec {v}}_{1}=\left({\begin{array}{c}1\\5\end{array}}\right),\;\;{\vec {w}}_{1}=\left({\begin{array}{c}4\\2\end{array}}\right),\,\!$

we get

${\vec {v}}_{1}+{\vec {w}}_{1}=\left({\begin{array}{c}1\\5\end{array}}\right)+\left({\begin{array}{c}4\\2\end{array}}\right)=\left({\begin{array}{c}5\\7\end{array}}\right).\,\!$

Multiplication by a Number

When a vector is multiplied by a number, each component is multiplied by that same number. For example, suppose

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

Then

$a{\vec {v}}=a\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)=\left({\begin{array}{c}av_{1}\\av_{2}\end{array}}\right).$

Length or Magnitude of a Vector

Consider the vector

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

We can calculate the length of a vector the same way that one calculates the hypotenuse of a right triangle. The magnitude is the square root of the sum of the squares of the entries. For example,

$|{\vec {v}}|={\sqrt {(v_{1})^{2}+(v_{1})^{2}}}.$

Figure V.1: The magnitude of a vector in terms of its entries.

Vectors of Length One, Unit Vectors

Vectors of length, or magnitude $=1$ are quite useful. These are also called "unit vectors". As we will see, they are used as "basis vectors" and also for quantum states. If a vector does not have length one, but it should have, then we can "normalize" it by dividing by the magnitude. When this is done, the vector of length one is often denoted with a "hat" ${\hat {v}}$ instead of the arrow ${\vec {v}}$. So

${\hat {v}}={\frac {1}{|{\vec {v}}|}}{\vec {v}}={\frac {1}{|{\vec {v}}|}}\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

The magnitude of this vector is

$|{\vec {v}}|={\sqrt {v_{1}^{2}+v_{2}^{2}}}.$

Then to see that the vector ${\vec {v}}$ is normalized,

${\begin{aligned}|{\hat {v}}|&={\sqrt {\frac {\vec {v}}{|{\vec {v}}|}}}\\&\\&={\sqrt {\left({\frac {v_{1}}{|{\vec {v}}|}}\right)^{2}+\left({\frac {v_{2}}{|{\vec {v}}|}}\right)^{2}}}\\&\\&={\frac {1}{|{\vec {v}}|}}{\sqrt {(v_{1})^{2}+(v_{2})^{2}}}=1.\end{aligned}}$

Notice that, in general, if the vector is multiplied by a number $a$ that is positive, then the magnitude of the vector is

$|a{\vec {v}}|={\sqrt {(av_{1})^{2}+(av_{1})^{2}}}={\sqrt {a^{2}(v_{1}^{2}+v_{2}^{2})}}=|a||{\vec {v}}|.$

So multiplying a vector by a number just changes the length, or magnitude, of the vector is $a$ is positive. If $a$ is negative, it changes the directions of the components and therefore of the vector itself and also changes the magnitude.

Dot Products or Inner Products

The inner product, or dot product, for two real two-dimensional vectors,

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right),{\mbox{ and }}{\vec {w}}=\left({\begin{array}{c}w_{1}\\w_{2}\end{array}}\right)$

or

${\vec {s}}=\left(s_{1},s_{2}\right),{\mbox{ and }}{\vec {u}}=\left(u_{1},u_{2}\right).$

can be computed as follows:

${\vec {v}}\cdot {\vec {w}}=v_{1}w_{1}+v_{2}w_{2},{\mbox{ and }}{\vec {s}}\cdot {\vec {u}}=s_{1}u_{1}+s_{2}u_{2}.$

For the inner product of ${\vec {v}}\,\!$ with itself, we get the square of the magnitude of ${\vec {v}}\,\!$, denoted $|{\vec {v}}|^{2}\,\!$:

$|{\vec {v}}|^{2}={\vec {v}}\cdot {\vec {v}}=v_{1}v_{1}+v_{2}v_{2}=v_{1}^{2}+v_{2}^{2}.$

If we want a unit vector in the direction of ${\vec {v}}\,\!$, we can simply divide it by its magnitude:

${\hat {v}}={\frac {\vec {v}}{|{\vec {v}}|}}.$

Now, of course, ${\hat {v}}\cdot {\hat {v}}=1\,\!$, which can easily be checked.

There are several ways to represent a vector. The ones we will use most often are column and row vector notations. So, for example, we could write the vector above as

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

In this case, our unit vectors are represented by the following:

${\hat {e}}_{1}=\left({\begin{array}{c}1\\0\end{array}}\right),\;\;{\hat {e}}_{2}=\left({\begin{array}{c}0\\1\end{array}}\right).\,\!$

$e_{1}\,\!$ and $e_{2}\,\!$ are called basis vectors. Notice they are unit vectors.

Any vector can be rewritten in terms of these basis vectors. For example,

${\vec {v}}=v_{1}{\hat {e}}_{1}+v_{2}{\hat {e}}_{2}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

We next turn to the subject of complex vectors and the relevant notation. We will see how to compute the inner product later, since some other definitions are required.

Complex Vectors

A complex vector is one that has complex numbers for entries. For complex vectors in quantum mechanics, Dirac notation is used most often. This notation uses a $\left\vert \cdot \right\rangle \,\!$, called a ket, for a vector. So our vector ${\vec {v}}\,\!$ would be

$\left\vert v\right\rangle =\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

For qubits, i.e. two-state quantum systems, complex vectors will often be used:

	${\begin{aligned}\left\vert \psi \right\rangle &=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\alpha \left\vert 0\right\rangle +\beta \left\vert 1\right\rangle ,\end{aligned}}$	(V.1)

where

	$\left\vert 0\right\rangle =\left({\begin{array}{c}1\\0\end{array}}\right),\;\;{\mbox{and}}\;\;\left\vert 1\right\rangle =\left({\begin{array}{c}0\\1\end{array}}\right)$	(V.2)

are the basis vectors. The two numbers $\alpha \,\!$ and $\beta \,\!$ are complex numbers, so the vector is said to be a complex vector. Recall from Chapter 1 that quantum states are represented by complex vectors, such as the quantum particle being in one of two different wells.

The Complex Conjugate of a Vector

To take the complex conjugate of a vector, each element of the vector has to be complex conjugated. So,

	${\begin{aligned}(\left\vert \psi \right\rangle )^{*}&=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{*}\\&=\left({\begin{array}{c}\alpha ^{*}\\\beta ^{*}\end{array}}\right)\\&=\alpha ^{*}\left\vert 0\right\rangle +\beta ^{*}\left\vert 1\right\rangle .\end{aligned}}$	(V.3)

The Transpose of a Vector

Let us reconsider the vector from above,

${\vec {v}}=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right).$

To transpose this vector, the vector will be turned into a row vector. It is the almost the same vector, just made into a row vector. The transpose is denoted with a superscript $T$:

${\begin{aligned}{\vec {v}}^{T}&=\left({\begin{array}{c}v_{1}\\v_{2}\end{array}}\right)^{T}\\&=\left({\begin{array}{cc}v_{1},&v_{2}\end{array}}\right).\end{aligned}}$

The Hermitian Conjugate, or "Dagger", of a Vector

The "dagger" of a vector, which is also called the hermitian conjugate, is the transpose and complex conjugate. This is denoted by a "dagger" superscript $^{\dagger }$

${\begin{aligned}({\vec {v}}^{*})^{T}&=\left({\begin{array}{c}v_{1}^{*}\\v_{2}^{*}\end{array}}\right)^{T}\\&=\left({\begin{array}{cc}v_{1}^{*},&v_{2}^{*}\end{array}}\right).\end{aligned}}$

In the case of complex vectors, the following notation is used:

	${\begin{aligned}(\left\vert \psi \right\rangle )^{\dagger }&=\left\langle \psi \right\vert \\&=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)^{\dagger }\\&=\left({\begin{array}{cc}\alpha ^{*},&\beta ^{*}\end{array}}\right).\end{aligned}}$	(V.4)

Complex Inner Product

To calculate the inner product of two complex, two-dimensional vectors, the complex conjugate of one is multiplied, term by term with the second. So if vectors ${\vec {v}}$ and ${\vec {w}}$ are complex vectors, the inner product, or dot product, is calculated by

${\vec {v}}\cdot {\vec {w}}={\vec {v}}^{\dagger }{\vec {w}}=v_{1}^{*}w_{1}+v_{2}^{*}w_{2}.$

This enables the inner product between two vectors to be written as

$(\langle {v}|)(|{w}\rangle )={\vec {v}}^{\dagger }{\vec {w}}=v_{1}^{*}w_{1}+v_{2}^{*}w_{2}.$

and the inner product of a vector with itself

$\langle \psi |\psi \rangle =\alpha ^{*}\alpha +\beta ^{*}\beta .$

Basis Vectors

Basis vectors are vectors that can be used to write any other vector. For example, any two-dimensional vector such as

${\begin{aligned}\left\vert \psi \right\rangle &=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\alpha \left\vert 0\right\rangle +\beta \left\vert 1\right\rangle ,\end{aligned}}$

can be written in terms of the two basis vectors $\left|0\right\rangle$ and $\left|1\right\rangle$. That is because

${\begin{aligned}\left\vert \psi \right\rangle &=\left({\begin{array}{c}\alpha \\\beta \end{array}}\right)\\&=\alpha \left({\begin{array}{c}1\\0\end{array}}\right)+\beta \left({\begin{array}{c}0\\1\end{array}}\right)\\&=\alpha \left\vert 0\right\rangle +\beta \left\vert 1\right\rangle ,\end{aligned}}$

and $\alpha$ and $\beta$ can be any numbers. So any vector can be written in terms of these.

It turns out that any pair of vectors that are orthogonal can serve as basis vectors. (In fact, any two that are not in the same direction.) Most of the time, it is best to use vectors that are orthogonal and normalized (have magnitude one). These are called orhtonormal vectors. The set of such vectors is called an orthonormal set and such a set can be found for any dimension. (The dimension is also the same number as the minimal number of vectors that we need in the set in order to be able to write any vector in terms of the basis vectors.)

It is easy to check that the vectors $\left|0\right\rangle$ and $\left|1\right\rangle$ are orthonormal. Another set of orthonormal vectors that are commonly used in quantum computing is the set

${\begin{aligned}\left\vert +\right\rangle &={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}1\\1\end{array}}\right)\\&={\frac {1}{\sqrt {2}}}(\left\vert 0\right\rangle +\left\vert 1\right\rangle ),\\\left\vert -\right\rangle &={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}1\\-1\end{array}}\right)\\&={\frac {1}{\sqrt {2}}}(\left\vert 0\right\rangle -\left\vert 1\right\rangle ).\end{aligned}}$

It is also easy to show that these two are also orthonormal. In addition, note that

${\begin{aligned}\left\vert 0\right\rangle &={\frac {1}{\sqrt {2}}}(\left\vert +\right\rangle +\left\vert -\right\rangle ),\\\left\vert 1\right\rangle &={\frac {1}{\sqrt {2}}}(\left\vert +\right\rangle -\left\vert -\right\rangle ).\end{aligned}}$

Exercises

To illustrate vector operations, let

$\left|r\right\rangle =\left({\begin{array}{c}1\\i\end{array}}\right),\;\;\left|s\right\rangle =\left({\begin{array}{c}1+i\\3\end{array}}\right),{\mbox{ and }}\left|t\right\rangle =\left({\begin{array}{c}-2i\\2\end{array}}\right).$

1. Vectors
1. Calculate the complex conjugate of $\left|r\right\rangle ,\;\left|s\right\rangle ,\;{\mbox{and}}\left|t\right\rangle .$
2. Calculate the magnitudes of all three vectors.
3. Normalize $\left|r\right\rangle ,\;\left|s\right\rangle ,{\mbox{ and }}\left|t\right\rangle$. Confirm that they are now unit vectors.
4. Calculate the Hermitian conjugate (dagger) of all three vectors.
2. Dirac Notation (bras, kets, and brackets)
1. Calculate the inner product $\left\langle s|t\right\rangle$, between $\left|s\right\rangle ,\;{\mbox{and}}\left|t\right\rangle .$
2. Calculate the inner products among all three vectors normalized versions of the vectors. Is there any pair that is orthogonal?
3. What can you say about the magnitude of the inner products in relation to the magnitudes of the individual vectors?
4. Find the inner product between $\left|0\right\rangle ,{\mbox{ and }}\left|1\right\rangle$ from Eq.(V.2).
3. Challenge Questions
1. Show that any vector can be written in terms of $\left|+\right\rangle ,\;{\mbox{and}}\left|-\right\rangle .$

Copyright

© Copyright 2022 BKR Collaboration