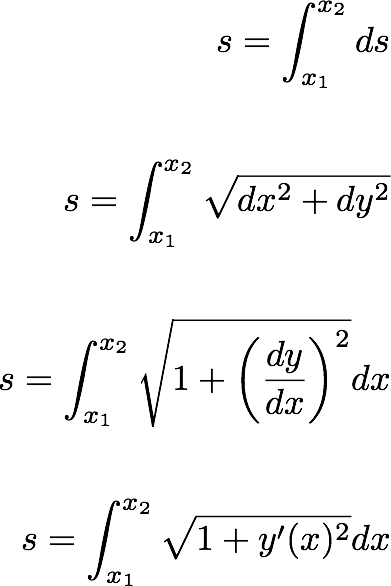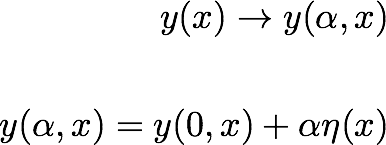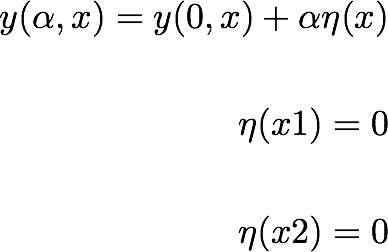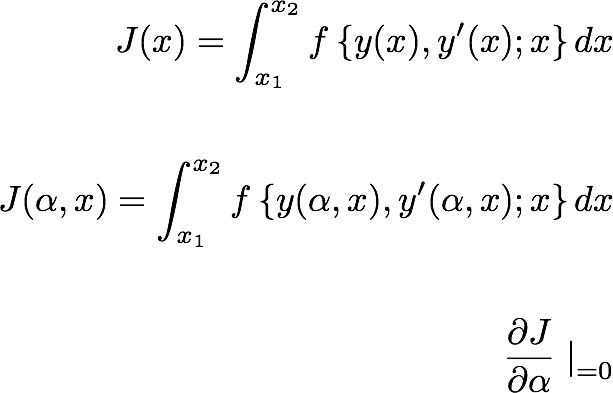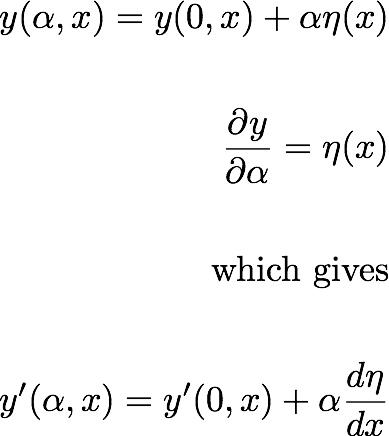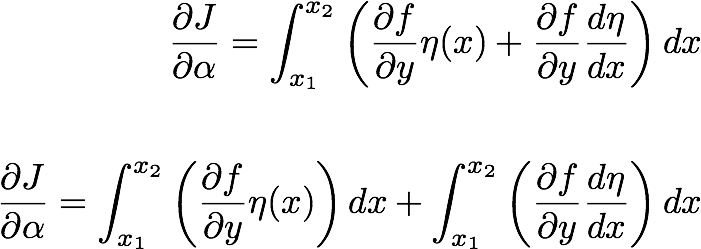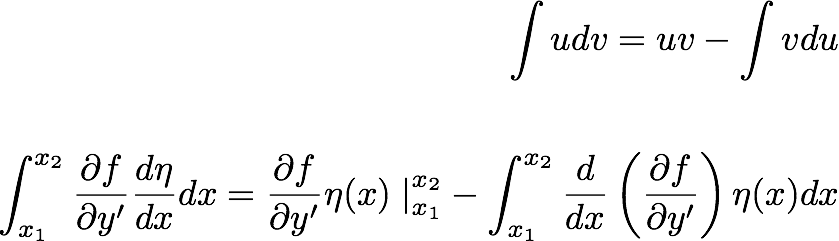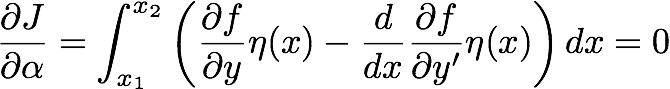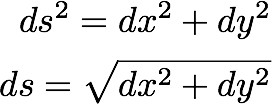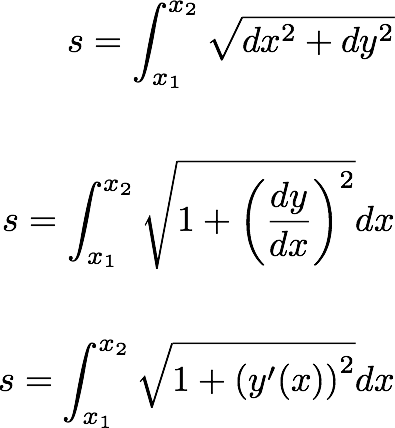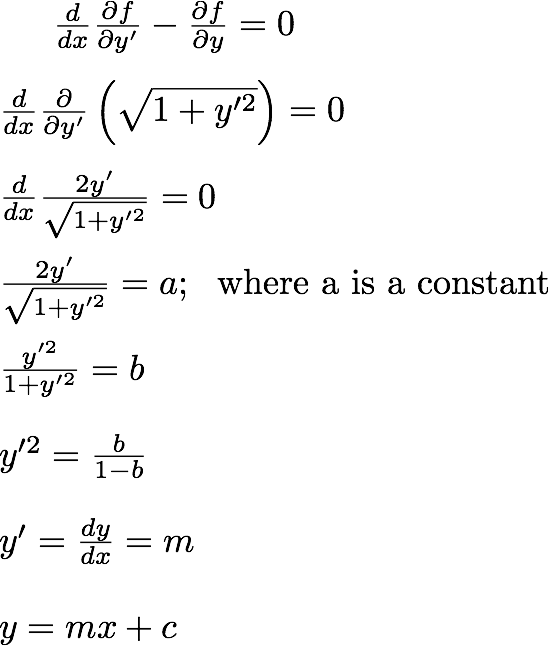DEpartment of physics

We start a new section today: Calculus of Variations. We discuss a little bit of the hostory of Calculus of variations. What is varying? Why we need a variational parameter.. etc. And  we provethe condition for extremizing an integral quantity. The result is known as the Euler's Equations. Finally we use Euler's equations to prove that the shortest path between two lines is given by a Straight line.

17.1 What is really the Calculus of Variation?
17.2 Problem of Quickest Distance of an Object
17.3 We need a variation parameter
17.4 Euler's Equations: Extermizing the Integral Quantity
17.5 Example: Shortest Distance between two Points in Two-Dimensional Plane

In the last few lectures, we discussed several classical motions and we used the Newtonian Mechanics to find out how a system evolve with time. As we have discussed earlier, Newton's Law is a Physical Law, Its proven right. But when the dynamics becomes complicated, it is not easy to apply the Newton's Laws. Alternative methods are required in this regard.

An alternate method to reach the equation of motions as given by the Newton's Law is Lagrane's equations. Lagrange's equations is based on the calculus of variation.

The calculus of variation basically provides us a way to find the conditions for minimizing a certain quantity which can be expressible as an integral. Basically we find the conditions for minimizing physical quantities such as: Time, length,  etc. 

17.1 What is really the Calculus of Variation?

The topic of calculus of variation is a problem in Mathematics with a long history. We want to find out the conditions for minimizing a certain quantity. Obviously, as the narure prefers to extermize certain quantities, this has applications in various fields, across from fundamental sciences to financial applications.

Didnt we know that we can minimize the quantity in particular problem by taking the derivative of that function with respoect to a variation parameter and making the derivative to zero. Well..... Yes, but here we are going to consider the extremization of not simple functions like f(x), but functionals, which can be written as a integral over some variables. We will talk about this in detail later.

Before going to details, let's talk about the historical problems that led to the Development of this field of calculus of variation.

RETURN TO TOP

17.2 Problem of Quickest Distance of an Object:
In a constant field, find the path between two points; Point A and B, that allows the particle to travel in the least amount of time. Bernouli has proposed this problem. How do we find an answer for this problem. This problem is known as the Brachistochrone probelm. (In Greek brachistos is shortest and chrone is time) --- (There's a long history about publishing this problem in 1696, After Bernouli submitted the problem, the answere were submitted by Newton, Bernouli (the brother of the Bernouli who submitted the problem) Leibniz etc....

Later other problems arose where a minimization of a certain integral quantity is important. For example, in Optics, light takes the path of quickest time, (which is known as the Fermat's Principle). This finding led to the reflection and refraction laws.

Let's talk about the shortest distance problem, sine it it easier to visualize. What is the shortest distance between two points? Well.... Now you know the answer... But imagine we did not know... How do we find it? It is another important question that led to the development of the field of calculus of variation.

Let's think about the problem of the shortest distance in a two-dimensional plane.

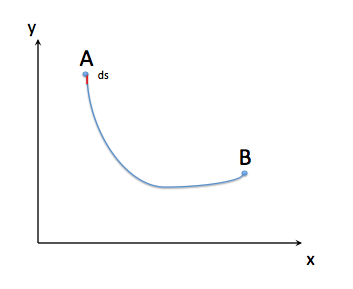
Let's see how we can find y(x), such that the distance between the two points along y(x) is minimized. Let's write an equation for y(x) and then see how we can minimize it.

Let's write the elemental distance along a random path is ds and which can be written as:

So the total distance would be;

So, now we have an equation for the total distance between the two points A and B. We want to find the y(x), that minimizes the distance s. How do we put it in to Mathematical formulation. We do not have the distance as a function of any parameter, so that we can tune the parameter until we minimize the distance. In other words, if we had a parameter, we could write the total distance betpeen two points as a function of the parameter, and then, take the derivative of the quantity we are trying to minimize with respect to this parameter,and make it to zero.

RETURN TO TOP

17.3 We need a variation parameter.

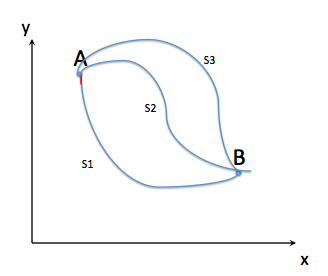
What would the parameter do? We introduce a parameter such that we can look for the integral quantity in the neighborhood of the optimal function. For example, if it is the shortest distance problem, we look for all possible different paths, (which are varied by a parameter) and then look for the path that gives the shortest distance.

You can represent this situation mathematically as follows.

In the above figure S1, S2, S3 are three possible total distances. Like wise, we can vary the path and look for the curve which gives a minimum S.

Let's put this situation in to mathematical formulations.

Basically, y(alpha,x) gives all possible functions as a paremetric representations. By varying the parameter alpha, we cover all possible forms of functions y(alpha,x).

The function is defined only between the two points x1 and x2. is a smooth function between the two end points. For alpha=0, we get the correct function.

RETURN TO TOP

17.4 Euler's Equations: Extermizing the Integral Quantity

Now we using this definition with the variational parameter, we can define the integral quantity, such as the distance.Let's call the integral quantity J;

----------------(17.1)       

we have defined:

Now by substituting these in the eq. (17.1):

-------------(17.2) 

For simplifying the second part, we can use the integration by parts,

So the first term in the above equations goes to zero, becuase we picked the variaational function to go to zero at the end points.

We then have:

-------------(17.3)

By combinning the equations (17.2) and (17.3), we get,

So, we get the condition for extremizing the integral quantity J as,

------------ (17.4)   

This equation is known as Euler's Equation, which is a necessary condition for J to be maximized.

Now we know the condition for extremizing J, Yet, we have not talked about how to define J, x, y,y' etc.

In order to apply Euler's equations, we need to identify the independent variable x, and the function to be minimized.

Let's do some examples:

RETURN TO TOP

17.5 Example: Shortest Distance between two Points in Two-Dimensional Plane

Now we  are going to use the Euler's equation to find out the distance between two points on a plane.

In order to apply Euler's equations, we need to define the problem. The quantity to be minimized is  the distance. Let's write the distance as an integral quantity.

An elemental length is 2D can be written as:

The total length between twopoints will be then,

Now let's use the Euler's equations to minimize s. By comparing to the above proof of Euler's equations:

Let's use EUler's equations:

We have above proved that, the shortest path betweentwo points can be written as y=mx+c, which we know is a straight line. We basically have used the Euler's equation to provea known condition here. We knew that shortest path between two points in a plane is a straight line.