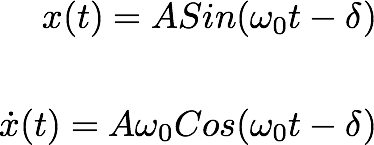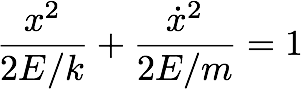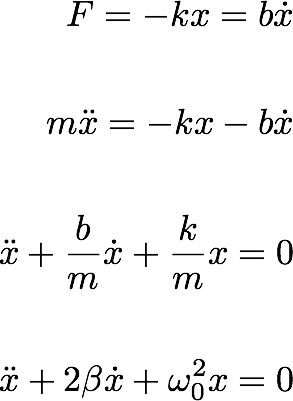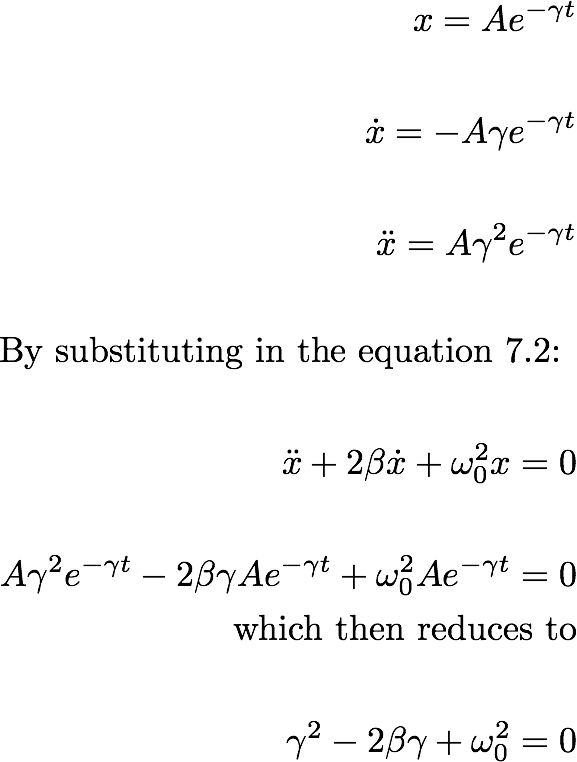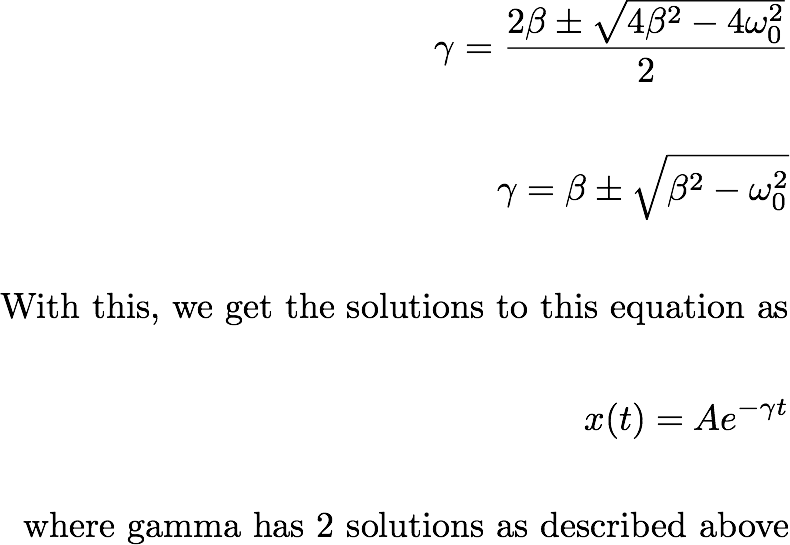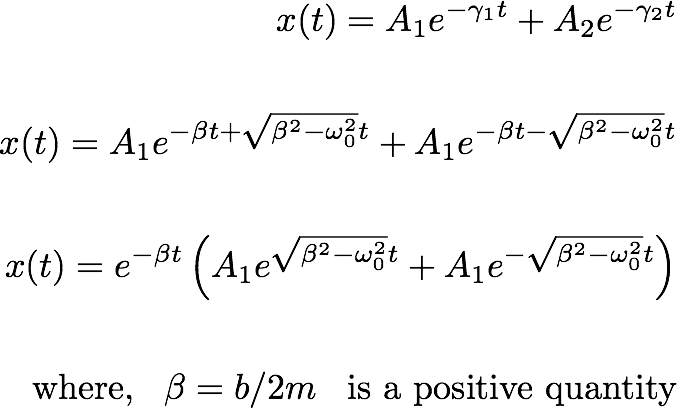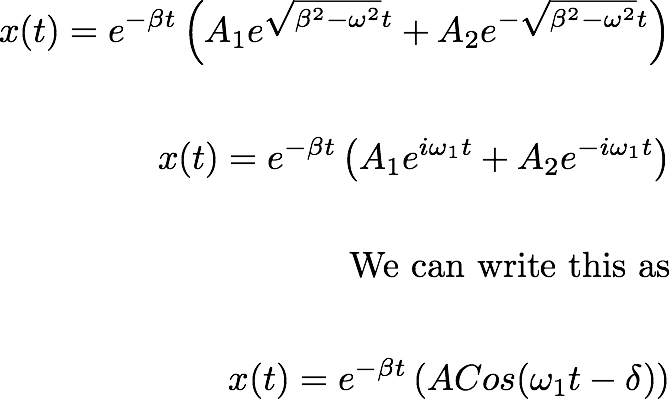DEpartment of physics

In this lecture, we will review about the Lissajous figures, those we have discussed in the last lecture, and talk more about how to define the state of an object in motion: The PhaseSpace will be introduces We will then discuss the effect of retarding forces on the small displacements of an object in equilibrium and with a restoring force. We will discuss the different levels of damping and work on the problem with underdamped conditions. Few Mathematica codes are available for understanding the under damped motion.

7.1 Harmonic Oscilliator in 2D - Lissajous Figures
7.2 PhaseDiagrams
7.3 Damped HarmonicOscillator
             Underdamped condition (with an interactive simulation)
7.1 Harmonic Oscilliator in 2D - Lissajous Figures.

In the last class, we discussed about the one-dimensional harmonic oscillator with no resistive force. We found thet for the Harmonic oscillator system, the total energy is conserved through out the motion. In fact. there is no dissipation. 

We have extended this idea to 2-Dimensions. We looked at how to draw the motion of the particle in x-y plane. For different frequencies in x and y directions, the x-y motion of the paticle takes different types of motion; those are called Lissajous Figures. We looked at different Lissajous figures. (And you will look at more in your home work.)

Different types of motions are possible depending on the relative ratio of the amplitude and the phase difference. (Look at the Lecture 6 for details).

Return to Top

7.2 PhaseDiagrams

The oscilliatory motion is explained by two quantities. How the velocity changes with space In fact, if you tell me the velocity as a function of time and the position as a function of time, I completely know the details about the motion. Because, given the position and the velocity at a particular time, you uniquely specify the state of the object at that given time. In fact, that is what you are doing in classical mechanics is trying to find out the state of the object, and try to find out how that state evolves with time.

Since the position and the velocity uniquely defines the state, we call it the phase space of the system. We can infact plot the phase diagrams in the phase space. All you need is to find how the velocity depends on the  position.

For instanct, let us talk about the one-dimensional Harmonic Oscillator Problem:

If we eliminate t from the above equations, we find a relationship between the position and the velocity.

----------------- (7.1)     

For a given total energy, the system defines a particular path. (Note also that two paths will not cross each other). That is because, if two paths cross each other, that means given that initial condition at the crossing point, the object may take two paths. In other words, it says, Newton's equation will not have a unique solution, which is not true.

For a given energy, the path defines by the equation 7.1 represents an ellipse. For different energies, the phase space is a series of ellipses. Phase space becomes even more interesting when there are resistive force, which we will discuss at the end of this lecture.

Return to Top

7.3: Damped Oscilliations

The motion we have discussed so far are free oscillations. An object which is displaced (by a small amount) from its equilibrium position, which us then subjected to a restoring force. We restricted ourselves only to a linear force, (Hook's Law type of force).

Here we study the effect of retarding force on the motion we described previously.  The resistive or retarding force can take any complicated form. We will only look at the simple form of frictional forces. Let's assume that the frictional force is proportional to the instantaneous velocity of the object, and always act opposite to the motion.

Now let's write the Newton's equation for this motion.

-------------------- (7.2)       

Let's assume a solution of the form

----------------- (7.3)      

Equation (7.3) gives quadratic equation of gamma. We can get the solution to this quadratinc equation as:

So the general solution forthe position can be written as:

----------------- (7.4)           

So in the above equation, the exponentially decaying function represents an exponentially decaying function. In fact, there is this exponentially decaying function which acts as an envelope function for the function given by the quantity inside the paranthesis in equation 7.4.

Now let's talk about the function given by the paranthesis in the position function:

--------------------- (7.5)           

The characteristics of the above function totally depends on the relative dependance of the quantities b (damping coefficient) and k (which decides the magnitude of the restoring force).
The behaviour of the function in the equation (7.5) can be divided into three types of solutions.

Let'slook at the Under Damped Condition first.

-------------------- (7.6)      

Let's look at this equation in detail. Because of the exponentially decaying functions, which is an envelope function to the position coordinate, the change position coordinate is not periodic. Particle passes through the same position in different times. However, particle does not pass through the same position with the same velocity. That means, the state particle which has the damping force never repeat the same state.

However,in the above equation 7.6, we have defined an angular frequency \omega_1. Since there is no periodic motion as explained above, we cannot really define a frequency. Basically, omega related to the time difference beween the times that the particle crosses the origin.

Let's plot the position coordinate for the damped Harmonic Oscillator for the underdamped case.

The above CDF simulation is created by Thushari Jayasekera

In the previous cdf player, (hopefully) you have been able to look at how the position coordiante is affected by a retarding force. When there are no retarding forces, the position and the velocity are out of phase, they both change periodically. We proved in the previous chapter that the phase space is elliptical.

Let's look at the phase space diagrams for a underdamped harmonic oscillator.

The above CDF simulation is created by Thushari Jayasekera