DEpartment of physics

LEARNING GOALS: To identify the independent stiffness constants required to characteris elastic properties of solids Discuss how symmetry reduces the number of Stiffness constants needed - In particular, we will discuss the number of independent stiffness constants required to characterize elastic properties of solids with cubis symmetry. Relate Stiffness constants to Elastic Coeffiecients: We derive an equation for Compressibility/Bulk Modulus of Cubic systems Elastic Wave propagation in cubic crystals

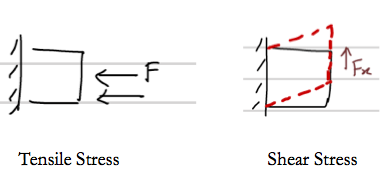
In the last class, we defined 6 stress components and 6 strain components to characterize the deformation in a solid. Strain is the response to Stress.

Three of the Stress components are Tensile and other three are Shear.

Strain and Stress are related by elastic constants.

There are 6 strain components. $e_{xx},e_{yy}, e_{zz}$ are 3 tensile strains and thre strains are $e_{yz},e_{zx},e_{xy}$$aree_{yz},e_{zx},e_{xy}$

A tensile stress can make a shear strain. Also a shear stress can create a tensile strain. That give 36 possible elastic constant to relate stress and strain.

Hooke's law states that for small deformations, the strain is directly proportional to stress (Linear Regime).  Recall Hooke's Law for a spring. $$ F=kx$$

In the similar way, we can write: $$\begin{eqnarray} e_{xx}=S_{11} X_x+ S_{12} Y_y + S_{13} Z_z + S_{14}Y_z + S_{15} Z_x + S_{16} X_y \\\nonumber e_{yy}=S_{21} X_x+ S_{22} Y_y + S_{23} Z_z + S_{24}Y_z + S_{25} Z_x + S_{26} X_y \\\nonumber e_{zz}=S_{31} X_x+ S_{32} Y_y + S_{33} Z_z + S_{34}Y_z + S_{35} Z_x + S_{36} X_y \\\nonumber e_{yz}=S_{41} X_x+ S_{42} Y_y + S_{43} Z_z + S_{44}Y_z + S_{45} Z_x + S_{46} X_y \\\nonumber e_{zx}=S_{51} X_x+ S_{52} Y_y + S_{53} Z_z + S_{54}Y_z + S_{55} Z_x + S_{56} X_y \\\nonumber e_{xy}=S_{61} X_x+ S_{62} Y_y + S_{63} Z_z + S_{64}Y_z + S_{65} Z_x + S_{66} X_y \\\nonumber \end{eqnarray}$$

The S's are called Elastic Compliance Constants or Elastic Constants.

We can also invert this equation to get:
$$ \begin{eqnarray} X_{x}=C_{11} e_{xx}+ C_{12} e_{yy} + C_{13} e_{zz} + C_{14}e_{yz} + C_{15} e_{zx} + C_{16} e_{xy} \\\nonumber Y_{y}=C_{21} e_{xx}+ C_{22} e_{yy} + C_{23} e_{zz} + C_{24}e_{yz} + C_{25} e_{zx} + C_{26} e_{xy} \\\nonumber Z_{z}=C_{31} e_{xx}+ C_{32} e_{yy} + C_{33} e_{zz} + C_{34}e_{yz} + C_{35} e_{zx} + C_{36} e_{xy} \\\nonumber Y_{z}=C_{41} e_{xx}+ C_{42} e_{yy} + C_{43} e_{zz} + C_{44}e_{yz} + C_{45} e_{zx} + C_{46} e_{xy} \\\nonumber Z_{x}=C_{51} e_{xx}+ C_{52} e_{yy} + C_{53} e_{zz} + C_{54}e_{yz} + C_{55} e_{zx} + C_{56} e_{xy} \\\nonumber X_{y}=C_{61} e_{xx}+ C_{62} e_{yy} + C_{63} e_{zz} + C_{64}e_{yz} + C_{65} e_{zx} + C_{66} e_{xy} \\\label{one} \end{eqnarray} $$


The C's are called Elastic Stiffness constants.

At this point, we have defined 36 elastic constants to characterize elastic properties of solids. How many of them are indemendent. We need the minumum number of cosntants to characterize the elastic properties of solids.

Elastic Energy Density

We just defined a set of constants. We do not know how they relate to physical quantities. Now we are going to write the elastic energy density stored in the system as a result of the deformation. Let's recall the spring problme i the Hooke's law limit. When the spring is stretched or compressed by x, the elastic energy stored in the spring was found to be: \[ U=\frac{1}{2} kx^2 \]

Elastic density is a quadratic function of strain.  Following that, we can write the elastic energy stored in a deformed solid as:

\[ \begin{equation} U=\frac{1}{2}\sum_{1}^{6} \sum_{i}^{6} \tilde{C}_{\lambda,\mu} e_{\lambda} e_{\mu} \end{equation} \] 

 ----------------------------------------------------------------------- (1)

Notice that we used the running index 1 to 6, which are defined as:

$$ 1 \rightarrow xx, 2 \rightarrow yy, 3 \rightarrow zz, 4 \rightarrow yz, 5 \rightarrow zx, 6 \rightarrow xy $$

Also notice that, we have not used C, but C with a tilde. Because we do not know how the constants should appear in the elastic energy density.

We can expand the energy term, [According to eq(1) ]:

$$ U=\frac{1}{2} \tilde{C}_{11} e_1 e_1  + \frac{1}{2} \tilde{C}_{12} e_1 e_2 + \frac{1}{2} \tilde{C}_{21} e_2 e_1 +\frac{1}{2} \tilde{C}_{13} e_1 e_3 +\frac{1}{2} \tilde{C}_{31} e_3 e_1 + \cdots $$ 

 -------------------------------------------------------------------- (2)

The stress components are the derivative of U with respect to the associated strain component:

$$ X_x = \frac{\partial }{\partial e_1} U \,\,\, = \,\,\, \tilde{C}_{11} e_1 +\frac{1}{2} \left( \tilde{C}_{12}+\tilde{C}_{21}\right) e_2 +  \frac{1}{2} \left( \tilde{C}_{13}+\tilde{C}_{31}\right)e_3 + \cdots$$

We can also write in the condensed form as:

$$ X_x=\tilde{C}_{11} e_1 + \sum_{\beta=2}{6} \left( \tilde{C}_{1\beta}+\tilde{C}_{\beta 1}\right) e_{\beta} $$

What are we la=earning here? The coefficients C's do not appear in physical quantities. What appears is

$$ \frac{1}{2}\left(\tilde{C}_{\alpha \beta } + \tilde{C}_{\beta \alpha} \right) $$

That means we can define Elastic Constants symmetrically.

We will use

$$ C_{\alpha \beta}= \frac{1}{2}\left(\tilde{C}_{\alpha \beta } + \tilde{C}_{\beta \alpha} \right) = C_{\beta \alpha} $$

That means, since the elastic constants can be defined symmetrically, we do not need 36 independent constants. That comes down to 21.

OK, At this point, what we defined

• 6 Stress Components
• 6 Strain Components
  
• Stress and Strain components are related through 21 independent elastic stiffness constants.
  

In summary, what we got is:

 $$\begin{bmatrix} X_x \\ Y_y \\ Z_z \\ Y_z \\ Z_x \\ X_y   \end{bmatrix}=  \begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16}  \\ C_{12} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ C_{13} & C_{23} & C_{33} & C_{34} & C_{35} & C_{36} \\
C_{14} & C_{24} & C_{34} & C_{44} & C_{45} & C_{46} \\ C_{15} & C_{25} & C_{35} & C_{45} & C_{55} & C_{56} \\C_{16} & C_{26} & C_{36} & C_{46} & C_{56} & C_{66}    \end{bmatrix}\begin{bmatrix} e_1 \\ e_2 \\ e_3 \\ e_4 \\ e_5 \\ e_6   \end{bmatrix}$$




Now we need to further analyze the elastic constants for particular symmetries. That means, How many independent quantities we need to characterize elastic properties of Cubic crystalline solid? ... etc.

Elastic Stiffness Constants of Cubic Crystals

Let's write the elastic energy term again:

$$U = \frac{1}{2} C_{11} e^2_{xx} + \frac{1}{2} C_{22} e^2_{yy}+\frac{1}{2}C_{33}e^2_{zz}+\frac{1}{2}C_{44}e^2{yz}+\frac{1}{2}C_{55}e^2_{zx}+\frac{1}{2}C_{66}e^2_{xy}+C_{12} e_{xx}e_{yy}+C_{13}e_{xx}e_{zz}+C_{21}e_{yy}e_{xx}+C_{23}e_{yy}e_{zz}+C_{31}e_{xx}e_{zz}+C_{32}e_{zz}e_{yy}+ \text{Other quadratic Terms} $$

 -------------------------------------------------------------------- (3)

These other quadratic terms include terms like: $$\frac{1}{2}C_{14}e_{xx}e_{yz} + \frac{1}{2}C_{15}e_{xx}e_{zx}+\frac{1}{2}C_{16}e_{xx}e_{xy}+ \cdots$$

 -------------------------------------------------------------------- (4)

We know that cubic systems has a crystalline symmetry. 

That means if we do the change $x→y→z→x$ (there are other equivalent changes), the elastic energy should not be different. That is Physical properties of a cubic crystalline solid is invariant under 2 $∏$rotation./3 rotation about [111] direction.

The terms marked in eq. (3) will satisfy that condition only if $C_{11}=C_{22}=C_{22},$ $C_{12}=C_{13}$and $C_{44}=C_{55}=C_{66}$

which gives:

$$ U=\frac{1}{2}C_{11}\left( e^2_{xx}+e^{2}_{yy}+e^2_{zz}\right) + \frac{1}{2}C_{44}\left(e^2_{yz}+e^2_{zx}+e^2_{xy}\right)+C_{12}\left(e_{yy}e_{zz}+e_{zz}e_{xx}+e_{xx}e_{yy}\right)$$

And the terms include in eq.(4) will not be invariant under cubic symmetry. So all the elastic constant appear in eq.(4) (all of which are not explicitly written) should go to zero. Now we can write the elastic stiffness constants for a material with cubic cymmetry as:

 $$  \begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0  \\ C_{12} & C_{11} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{12} & C_{11} & 0 & 0 & 0 \\
C_0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{44}    \end{bmatrix}$$

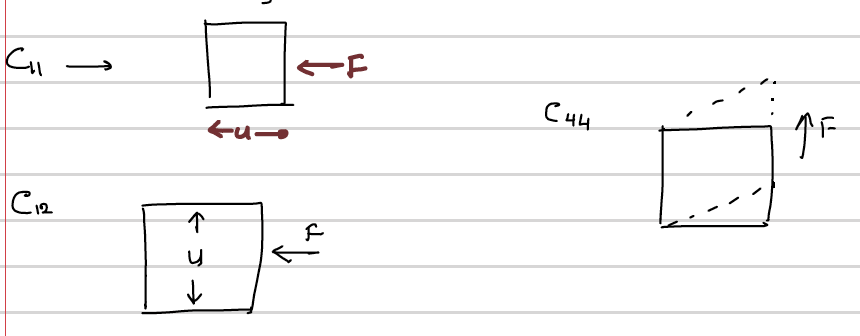
We only need 3 independent elastic constats to describe deformation in cubic crystals. The deformations associated with these three constants are visualized below.

Elastic Coefficients of Cubic Crystals

We can write the elastic coeeficeints of cubic crystals using those three independent elastic constants we defined. Here we do one example (Following Kittel).
Bulk Modulus characterizes the resistance of a matrial to pressure, and defined as $B=-V\frac{dP}{dV}$. Compressibility is the inverse of Bulk Modulus.
 Let's consider a uniform dilation of a solid  : $e_{xx}=e_{yy}=e_{zz}=\delta/3$

$$ U=\frac{1}{2}C_{11}\left( e^2_{xx}+e^{2}_{yy}+e^2_{zz}\right) + \frac{1}{2}C_{44}\left(e^2_{yz}+e^2_{zx}+e^2_{xy}\right)+C_{12}\left(e_{yy}e_{zz}+e_{zz}e_{xx}+e_{xx}e_{yy}\right)$$

$$U=\frac{1}{2}C_{11} \left(3 \frac{\delta^2}{9}\right) + \frac{1}{2} C_{44}(0)+C_{12}\left(3 \frac{\delta^2}{9}\right)$$

which simplifies to

 $U=\frac{1}{6}C_{11}\delta^2+\frac{a}{3}C_{12}\delta^2$

$$U=\frac{1}{6}\left(C_{11}\delta^2+2 C_{12}\delta^2\right)$$

Stress can be calculated as:

$$\frac{\partial U}{\partial e_{xx}}=\frac{1}{6}\left(C_{11}+2C_{12}\right) 2 \delta $$

And now we can consider the change in volume, which is the response to the stress.

$$\frac{dV}{V}=\frac{V'-V}{V}=\frac{\vec{x}'.\vec{y} \times \vec{z}'-\vec{x}.\vec{y}\times \vec{z}}{\vec{x}.\vec{y}\times\vec{z}}$$

By substituting the values, we can get: $\frac{dV}{V}=e_{xx}+e_{yy}+e_{zz}=\delta$

Then

 $$

$$

$B=\frac{\frac{1}{3}\left(C_{11}+2 C_{12}\right) \delta}{\delta}=\frac{1}{3}\left(C_11+2C_{12}\right)$

Elastic Wave Propagation in Cubic Crystals

This is going to be the last topic we discussed within continuum approximation.


The positions of atoms in a solid change as a response external
stress. Now we are interested in the variation of this displacement
vector as a function of time. We are basically going to apply F=ma.


Let's consider a cub of volume $$ \Delta x \Delta y \Delta z$$ acted
upon by a stress $X_x(x)$. The stress will be a function of x. That's
why a given mass experience a net force, and the displacement vector
change.

The stress at a position $$x+\Delta x$$ can be written as:

$$ X_x(x+\Delta x)=X_x(x)+\frac{\partial }{\partial x} X_x \Delta x $$

The net force on the system is therefore:

$$\frac{\partial }{\partial x} X_x  \Delta x \Delta y \Delta z$$.

That is the stress in x direction on the surface perpendicular to
x-axis.  There are net forces in x direction due to shear forces as
well.

The total force on the mass in x-direction :

$$F(x)=\left(\frac{\partial }{\partial x}X_x + \frac{\partial
}{\partial y}X_y  + \frac{\partial }{\partial z}X_z \right) \Delta x
\Delta y \Delta z$$

Knowing the total force acting in x direction on mass $$\Delta x
\Delta y \Delta z$$, we can now apply F=ma for the motion.

$$m \frac{\partial ^2}{\partial t^2} u = =\left(\frac{\partial
}{\partial x}X_x + \frac{\partial }{\partial y}X_y  + \frac{\partial
}{\partial z}X_z \right) \Delta x \Delta y \Delta z $$

$$\rho \Delta x \Delta y \Delta z \frac{\partial ^2}{\partial t^2} u =
=\left(\frac{\partial }{\partial x}X_x + \frac{\partial }{\partial
y}X_y  + \frac{\partial }{\partial z}X_z \right) \Delta x \Delta y
\Delta z $$,

where $\rho$ is the mass density. The above equation simplifies to:

$$\rho \frac{\partial ^2}{\partial t^2} u = =\left(\frac{\partial
}{\partial x}X_x + \frac{\partial }{\partial y}X_y  + \frac{\partial
}{\partial z}X_z \right)  $$,

u is the component of displacement in the x direction. Simillarly

The above CDF was created by Thushari Jayasekera, (Some ideas were adopted from the simulation made by Craig Carter
http://demonstrations.wolfram.com/PhononDispersionRelationInBrillouinZone/