Main Content Area
Lecture
2
2.1 Kinematic Equations (Quick
Review)
- At the end of this lecture, you will be able to refresh your knowledege on how the Kinematic Equations can be used to analyze motion of an object. We will discuss when Kinematics equations are limited and thus the importance of Newton's equations of motion for understanding the dynamics of a particle.
- We will also discuss the conditions under which the Newton;s laws are valid. We will start applying the Newtons equations for studying particle dynamics with a simple example.
2.2 Concept of Force
2.3 Physical Laws
2.4 Newton's Laws of Motion
2.5 Inertial Mass and Gravitational Mass
2.6 Frames of Reference
2.7 The Dynamics of a particle using Newtonian Mechanics: Examples
2.1 Kinematic Equations (Quick Review)
Let's re-visit the most popular problem in Classical Mechanics: The Projectile Motion. How did we solve this problem? We use the Kinematic Equations.
What are Kinematic Equations. Kinematic equations are the result of definning the average accelleration for a motion of a particle.
As a particle moves from one point to another along some path, the instantaneous velocity changes.
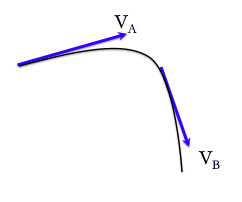 for the motion between the
points A and B, we can define an average accelleration:
for the motion between the
points A and B, we can define an average accelleration:If the average accelleration change from
one time interval to another, that means, we cannot define
such average accellerations, In that case, we have to
define an instantaneous accelleration.
So for motions which are subjected to constant accellerations, we can start with the definition of accelleration in equation (1.1), and find out a set of equations as:
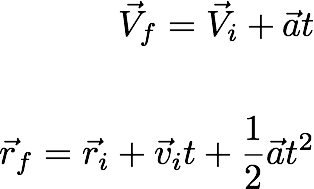
----------------
(1.2)
The set of equations as shown in the
equation (1.2) are know as Kinematic Equations. The
only information we use is the definition of average
accelleration.
Thus, it is clear that, Kinematic equations can be used to analyze a motion which has a constant accelleration throughout the motion.
For example the Simple Projectile Motion.
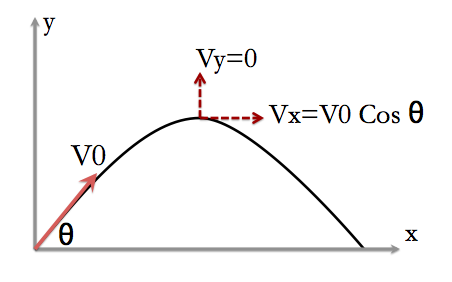
Thus, it is clear that, Kinematic equations can be used to analyze a motion which has a constant accelleration throughout the motion.
For example the Simple Projectile Motion.

For the projectile motion,
The average accelleration in y diretion:
The average accelleration in x direction:
Since the particle is subjected to a constant accelleration, you can apply Kinematic equations.
What we know:
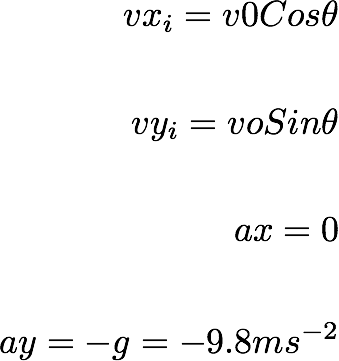
So we can apply the Kinematic equations in x and y directions separately.
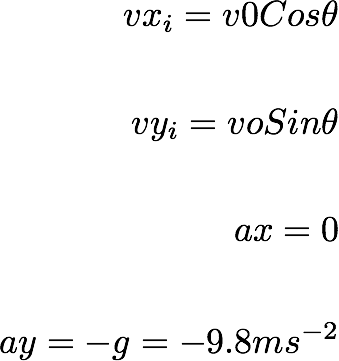
So we can apply the Kinematic equations in x and y directions separately.
In the previous problem, we discussed how the motion of a particle change. What cause this change. That is the beginning of the concept of force.
2.2 The Concept of Force
The force refers to an interaction with an object (Well.... interaction of two objects) and create some changes in the velocity. There are different types of forces.
- Gravitational Force
- Electromagnetic Force
- Strong Force
- Weak Force
So, How do you relate the magnitude of the force to the
change in the change in motion. Newton's
Laws gives a qualitative and quantitative idea for the
force.
2.3 What is a Physical Law?
Physical laws are based on experimental facts. Once a set of experimental data has been correlated and a postulate has been formulated, regarding the phenomena to which the data refer, then various implications can be worked out. If these implications are all verified by experiments, the postulate becomes a Physical Law.
Newton provided us with the fundamental laws of mechanics.
2.4 Newton's Laws of Motion
Law I:
A body remains at rest or in uniform motion unless acted upon by a force
This law is worded differently in different text books. For example "SERWAY and JEWETT: Physics for Scientists and Engineers" word is as: "If an object does not interact with other objects, it is possible to identify a reference frame in which the object has the zero accelleration". Such a frame is called an inertial frame of reference.
Law II:
A body acted upon by a force moves in such a manner that the time rate of change of momentum equals the force.
Law III:
If two bodies exert forces on each other, these forces are equal in magnitude and opposite in direction
The first law itself gives a qualitative idea about the force. (In fact, the first law explains the situation for "zero force"). A body moving with no force acting upon them is called a free body or a free particle. (When we say the object is in uniform motion or at rest, we need to specify with respect to which frame. Where do you measure the quantities from? We will talk about this fact; the reference frames in a latter section)
The second law is an explicit statement of force. The momentum is defined as:
Therefore the Newton's second law can be
mathematically expressed as:
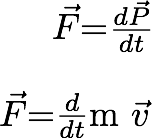
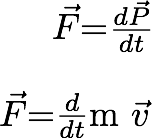
The second law in
other words tells, the accelleration is directly
proportional to the external force and inversely
proportional to the mass.
Third law is not general. The law
applies when the force exerted by one object on another
object is directed along the line connecting the
objects. (Central Forces). For example: The force
between two static charges obey the Newton;s third law:
But the force between two moving charges do not. In the
latter case the force is velocity dependant.
Let's do a simple numeric example to understand the Newton's second Law.
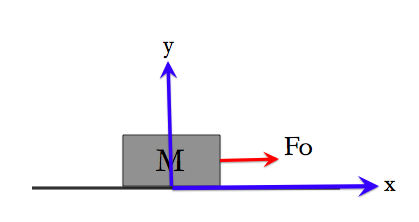
Let's first make a Free-Body digram and gather the information
2.5 Introduction to Inertial Mass and Gravitational Mass:
The second law also gives an idea about the mass. Mass is an intrinsic property of a body which is a measure of how much the object can resist to the changes of motion.
Let's consider two isolated bodies. If the body 1 exert a force F12 on the body 2, the body 2 exter a force F21=-F12 on body 1. By applying the Newton's second law, we then get:
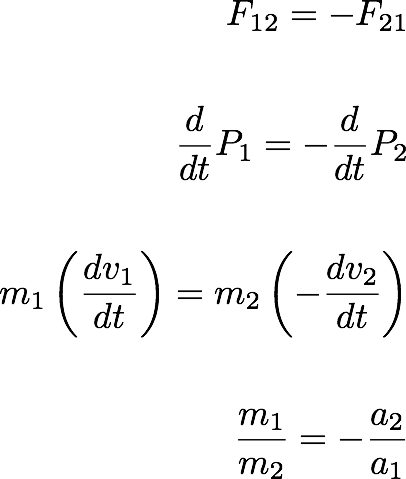
2.6 Frames of Reference:
In order for the above laws to make a omplete sense, we have to measure the quantities of motion. The quantities have to be measures with relative to a reference frame.
A reference frame is called an Inertial Frame, if the Newton;s laws are valid in that frame.
If Newton's laws are valid in one reference frame, then they are also valid in any other reference frame in uniform motion with relative to the first. (That is because, Newton;s laws has the accelleration term in it). The change of cooridnates which has a constant velocity term in it will not have any effect on the acceleration.
What is then a practical intertial frame of refernece frame?
The earth is moving with relative to the other planets. So we may consider the "fixed" stars to define a frme that approximates an "absolute" inertial frame to an extent sufficient for the practical purposes.
Now we know that, the Newton's equations are valid only if we measure the quantities with relative to an inertial frame of reference. However. some times it becomes more convenient to measure the quantities with relative to non-intertial frames of reference. The method of applying Newton's Laws using quantities measured with relative to a non-inertial frame of reference will be discussed in a later chapter.
Let's do a simple numeric example to understand the Newton's second Law.
| EXAMPLE:
An object is at rest on a smooth horizontal
surface at time t=0. A constant force Fo
is applied on the object in the x direction. (a) What is the acceleration of this object? Is it a constant acceleration? (b) What is the velocity of the object at t=to? (c) What is the position coordinate of the object at time t=to with relative to the original position? |
Let's first make a Free-Body digram and gather the information

We have set up a coordinate system
and marked all the horizontal forces on the object.
By applying the newton;s second Law in the x direction:
Fo= M a ------------------------------------ (1.1)
The accelleration of the object in x direction equals to Fo/M. And it is clear that this accelleration is a constant.
Because the accelleration is a constant through out the motion, we can apply the Kinematic equations to answer the rest of the questions.
Velocity:
Let's use the kinematic equation: Vf=Vi + at. (knowing Vi=0),
Let's use the Kinematic equation, xf=xi+Vi t + at2 /2
xi=0
xf=Vi t + at2 /2
Object starts from rest: so Vi=0,
Let's try tosolve this problem directly using the Newton's equations. (Ofcourse, in the previous case we used the Newton;s equations to find the accelleration of the object, That's where we start now)
Let's solve the problem by direclty integrating the Newton's Law
Let's start with the equation (1.1): Fo=M a

Now, inorder to get the velocity and position as a function of time, we integrate the Newton's equations as follows.

Now I want to find the position as a function of time, So I start with the velocity equation:

So we have done the same problem in two different methods. Which one is easier and shorter? Why do we bother about the longer way (by integrating the Newton's equation)
The answer is: There are some problems, that the Kinematic equations cant be applied. In which, the average accelleration is drastically different from one time interval to another. In those cases, we need to define instantaneous accelleration, not the average accelleration. And the Kinematics equations cannot be applied. We can investigate the motion by integrating the Newton't eqution.
Let's do another problem to convince ourselves.
Answer these questions in the Homework # 1.
By applying the newton;s second Law in the x direction:
Fo= M a ------------------------------------ (1.1)
The accelleration of the object in x direction equals to Fo/M. And it is clear that this accelleration is a constant.
Because the accelleration is a constant through out the motion, we can apply the Kinematic equations to answer the rest of the questions.
Velocity:
Let's use the kinematic equation: Vf=Vi + at. (knowing Vi=0),
The position of the object after time to:we get: Vf= a t = Fo t/M
So the velocity of the object at time t=to:
V (to)= Fo to /M
Let's use the Kinematic equation, xf=xi+Vi t + at2 /2
xi=0
xf=Vi t + at2 /2
Object starts from rest: so Vi=0,
We have completely solved the problem using the Kinematics equations.xf= at2 /2 =Fo to2/2M
Let's try tosolve this problem directly using the Newton's equations. (Ofcourse, in the previous case we used the Newton;s equations to find the accelleration of the object, That's where we start now)
Let's solve the problem by direclty integrating the Newton's Law
Let's start with the equation (1.1): Fo=M a

Now, inorder to get the velocity and position as a function of time, we integrate the Newton's equations as follows.

Now I want to find the position as a function of time, So I start with the velocity equation:

So we have done the same problem in two different methods. Which one is easier and shorter? Why do we bother about the longer way (by integrating the Newton's equation)
The answer is: There are some problems, that the Kinematic equations cant be applied. In which, the average accelleration is drastically different from one time interval to another. In those cases, we need to define instantaneous accelleration, not the average accelleration. And the Kinematics equations cannot be applied. We can investigate the motion by integrating the Newton't eqution.
Let's do another problem to convince ourselves.
| EXAMPLE:An
object is at rest on a horizontal surface at
time t=0, A time dependent force in the form
of Fo t /k is applied in the x-direction. (a) What is the accelleration of the object? Is it a constant? (b) What is the velocity of the object at time to? (c) How long the object has travelled within this time to? |
Answer these questions in the Homework # 1.
2.5 Introduction to Inertial Mass and Gravitational Mass:
The second law also gives an idea about the mass. Mass is an intrinsic property of a body which is a measure of how much the object can resist to the changes of motion.
Let's consider two isolated bodies. If the body 1 exert a force F12 on the body 2, the body 2 exter a force F21=-F12 on body 1. By applying the Newton's second law, we then get:
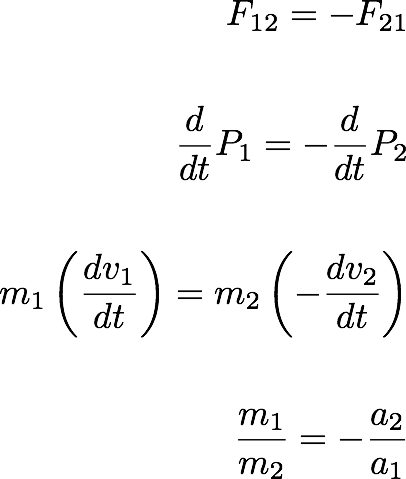
where, the negative sign says, the
two accellerations are opposite in direction. By
comparing the accellerations, we can get the ratio
of the masses of the objects. This mass is the
Inertial Mass: not to be confused with the
Gravitational Mass or the weight. Weight of a body
is the gravitational force acting on the body mg.
2.6 Frames of Reference:
In order for the above laws to make a omplete sense, we have to measure the quantities of motion. The quantities have to be measures with relative to a reference frame.
A reference frame is called an Inertial Frame, if the Newton;s laws are valid in that frame.
If Newton's laws are valid in one reference frame, then they are also valid in any other reference frame in uniform motion with relative to the first. (That is because, Newton;s laws has the accelleration term in it). The change of cooridnates which has a constant velocity term in it will not have any effect on the acceleration.
What is then a practical intertial frame of refernece frame?
The earth is moving with relative to the other planets. So we may consider the "fixed" stars to define a frme that approximates an "absolute" inertial frame to an extent sufficient for the practical purposes.
Now we know that, the Newton's equations are valid only if we measure the quantities with relative to an inertial frame of reference. However. some times it becomes more convenient to measure the quantities with relative to non-intertial frames of reference. The method of applying Newton's Laws using quantities measured with relative to a non-inertial frame of reference will be discussed in a later chapter.
The force on the particle can be any combination of position, velocity, and time and is generally denoted as F(r,v,t). The Goal is: given the type of the force, we need to find out how the position and velocity change as a function of time.
The approach is: We start with the Newton's equation:
Let's do some simple examples:
EXAMPLE 1 A Block sliding down a frictionless inclined plane:
A block is sliding down a frictionless plane, that is inclined by an angle theta . What is the accelleration of the block? What is the velocity of the block after it moves from rest a distance x0 down the plane?
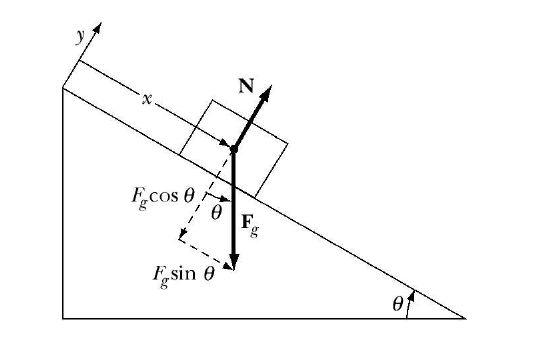
Fig. 1. A Block sliding down an inclined plane.
The General
approach for solving a problem:- Make a sketch of the problem, mark the forces and other known quantities |
Let's get back to the problem: A block sliding down the frictionless plane. The situation is sketched in the Figure 1.1. The forces acting on the plane:
- Gravitational ForceWe select a coordinate system, that is suitable for this particular motion. The block is consttrained to move along the plane. We select the coordinate system as shown in the figure 1.1.: +x down the plane.
- The planes normal force on the box
Let's start with this problem in the next class !!
