Main Content Area
Lecture
3
3.1 EXAMPLE 1: A
Block sliding down a frictionless inclined plane:
- In this lecture, we will START applying Newton's equations to investigate the dynamics of a particle. Let's start with two simple examples, a block sliding down a frictionless plane and a plane with friction. Notice that, both these problems can be solved using Kinematics equations. In the Homework # 1, you will do both these problems using the Kinematics equations.
- In addition to applying the Newtonian mechanics for the motion of a particle, you will alsolearn about the static and kinetic frictional coefficient.
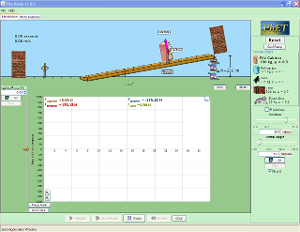
- There is an inetrative simulation embedded (from phET). In this lecture, you will ONLY see if you can open this simulation and play with it. (Just check the compatibility of these simulations in your computers and let me know)
- End of the class, we also discuss the other types of retarding force. We will do a problem with the velocity dependent ratarding force.
3.1 Example 1: A Block sliding down a frictionless inclined plane
3.2 Frictional Forces
- Static Frictional Coefficient
- Kinetic Frictional Coefficient
3.3 Example 2: A Block sliding down an inclined plane with a friction:
3.4 Other types of retarding forces
3.5 Retarding Forces in Horizontal Direction
A block is sliding down a frictionless plane, that is inclined by an angle theta . What is the accelleration of the block? What is the velocity of the block after it moves from rest a distance x0 down the plane?
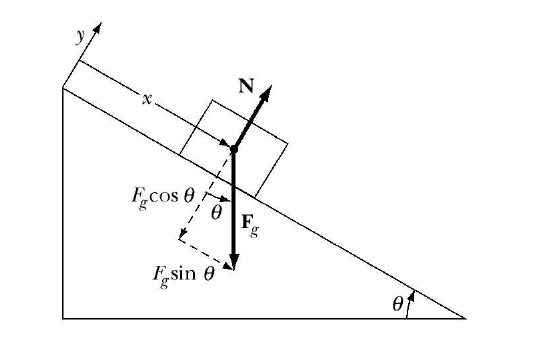
Last lecture, we discussed about the choice of our coordinate system (as shown in the figure) Now Mark the forces using the chosen coordinate system.
- The Normal force N is acting in the ŷ direction.
- The gravitational force Fg can be decomposed in to x and y directions.
Knowing the force acting on the system,
we can apply the Newton's second law of motion: Both in
x and y directions.
In y direction: There 's no accelleration in y direction.
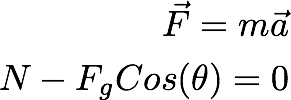
In x direction: There is an accelleration in the x direction. The only force in the x direction is coming from the gravitational force.
In y direction: There 's no accelleration in y direction.
In x direction: There is an accelleration in the x direction. The only force in the x direction is coming from the gravitational force.
Where ẍ is the acceleration along the x
direction, (That is what we are looking for):
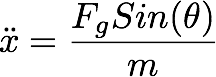
Now let's use the fact that the gravitational force equal mg, that

Now let's put the equation in the form:
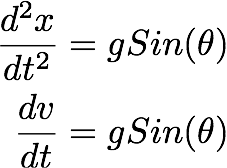
Now by integrating these equations and applying the boundary conditions, we can find out the equations of motion for the particle. That is how the velocity depend on time and how the position depend on time.
By integrating the above equation, we get:
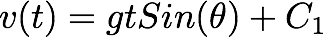
Let's write this equation as,
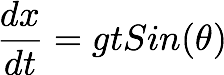
Now let's use the fact that the gravitational force equal mg, that
Now let's put the equation in the form:
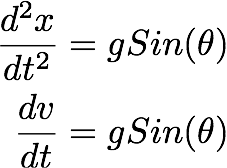
Now by integrating these equations and applying the boundary conditions, we can find out the equations of motion for the particle. That is how the velocity depend on time and how the position depend on time.
By integrating the above equation, we get:
where C1 is a constant.
We use the initial conditions (boundary conditions) to find the unknown integration constant C1.
At v(t=0)=0 and x(t=0)=0. The block starts with the zero velocity and we set the coordinate system such that at time t=0, the position coordinate of the block equals zero.
This conditions give C1=0: Now
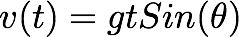 ------------------- (1)
------------------- (1)
We use the initial conditions (boundary conditions) to find the unknown integration constant C1.
At v(t=0)=0 and x(t=0)=0. The block starts with the zero velocity and we set the coordinate system such that at time t=0, the position coordinate of the block equals zero.
This conditions give C1=0: Now
Let's write this equation as,
By integrating again:
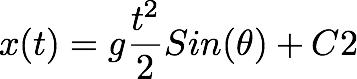
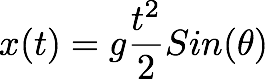 -------------------- (2)
-------------------- (2)
Now if we focus on the question, we want to find out the velocity of the block after it moves a x0 distance on the plane. So we need to write down the velocity as a function of the position (instead of as a function of time).
We can find t from equation (2) and substitute in the equation (1).
From (1):
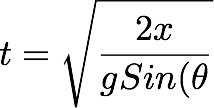
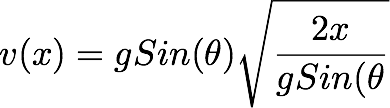
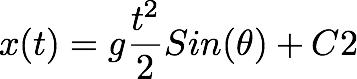
By considering the
initial condition, at t=0 x(t)=0 :
Therefore C2=0.
Now we have the position as a function of time:
Now we have the position as a function of time:
Now if we focus on the question, we want to find out the velocity of the block after it moves a x0 distance on the plane. So we need to write down the velocity as a function of the position (instead of as a function of time).
We can find t from equation (2) and substitute in the equation (1).
From (1):
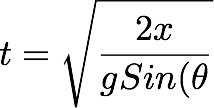
Substituting
that back in the equation (1):
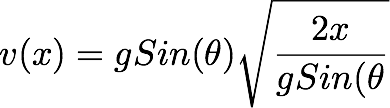
Finally, we get,
We can now find the velocity of the block at any position on the plane.
Frictional forces are occured when one surface is in touch with another surface. Frictional forces keep things from moving. These forces adjust itself to counter the force exerted to move the object. There is a point where the frictional force cannot excedd a particular maximum value. The maximum frictional force s obtained by the experimentally obtained formula:

where µs is the static frictional coefficient. In another words, the static frictional force gives the force needs to keep the object from moving.
When the object starts moving, there's still a frictional force that oppse the motion. This force is called the force of kinetic friction. Kinetic frictional force is usually less than the maximum static frictional force.
3.3 Example2: A Block sliding down an inclined plane with a FRICTION:
We can now find the velocity of the block at any position on the plane.
Frictional forces are occured when one surface is in touch with another surface. Frictional forces keep things from moving. These forces adjust itself to counter the force exerted to move the object. There is a point where the frictional force cannot excedd a particular maximum value. The maximum frictional force s obtained by the experimentally obtained formula:
where µs is the static frictional coefficient. In another words, the static frictional force gives the force needs to keep the object from moving.
When the object starts moving, there's still a frictional force that oppse the motion. This force is called the force of kinetic friction. Kinetic frictional force is usually less than the maximum static frictional force.
3.3 Example2: A Block sliding down an inclined plane with a FRICTION:
Return
to Top
The frictional force is in the -x direction, as shown in the figure. So the equation of motion in the y direction will remain the same.
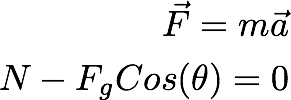
Now the equation of motion in the x-direction will be changed.
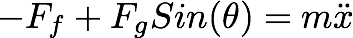
Let's visualize this problem in an interactive simulation.
------ PhET Simulation -------
Let's work
on the example.
If the
coefficient of friction
between the block and the
plane in the previous
example is µs=0.4, at what
angle will the block start
sliding if it initially is
at rest.
The frictional force is in the -x direction, as shown in the figure. So the equation of motion in the y direction will remain the same.
Now the equation of motion in the x-direction will be changed.
The
static friction force
keeps the block at rest.
As you increase the
angle, the Frictional
force increase. There is
a particular inclined
anlge, for which the
frictional force cannot
hold the block from
moving.
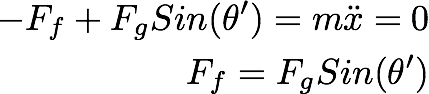
Given the fact that the
static frictional
coefficient equal 0.4,
we can calculate the
inclined angle of the
plane at which the block
start to slide. (The
angle for this problem
equals to 22 degrees.
Once the object start moving, we need to use the coefficient of Kinetic friction to calculate the frictional force.
Now
by using the form of
the frictional
force:
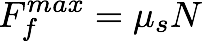
We
get:
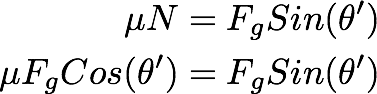
Once the object start moving, we need to use the coefficient of Kinetic friction to calculate the frictional force.
Let's visualize this problem in an interactive simulation.
------ PhET Simulation -------