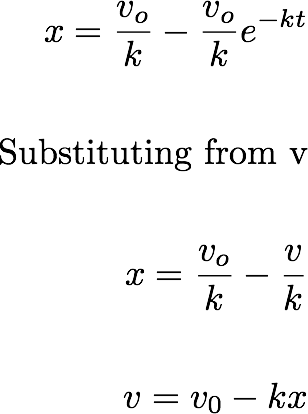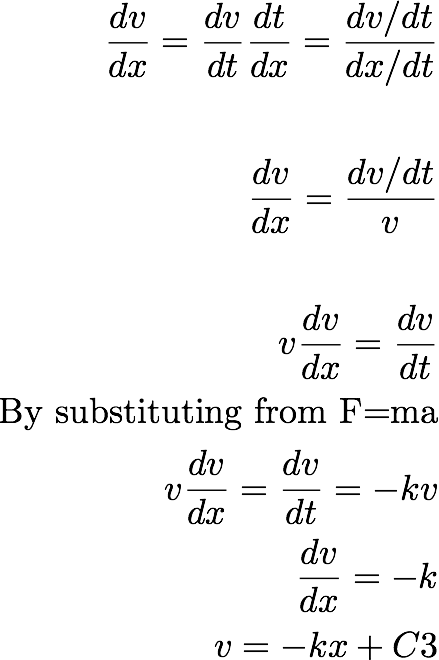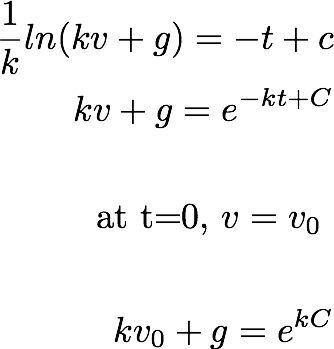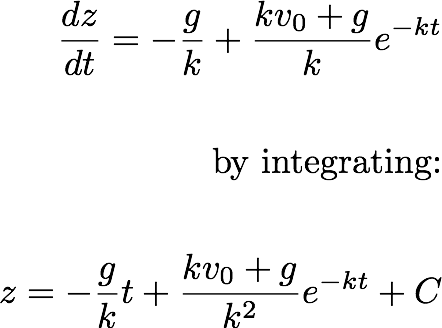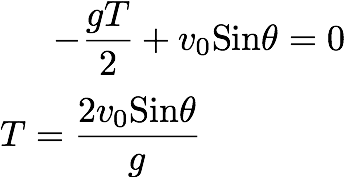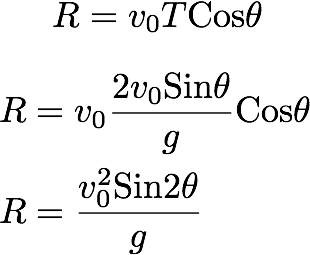DEpartment of physics

In the last lecture, we have applied the Newton's laws to investigate the dynamics of a block sliding on an inclined plane (both with friction and frictionless). In both cases, the total force is constant throught out the motion. In that case, we can analyze the motion by applying the Kinematic equations. But, in general, the force does not have to be a constant. In this lecture, we will discuss about one such non-constant force, the Retarding forces. We will learn in this problem, use of approximation methods when the problem becomes complicated.

4.1 More about the Horizontal motion of an object with a retarding force
4.2 Retarding forces on a Vertical Motion
4.3 Terminal Velocity
4.4 Projectile Motion with no Retarding Forces
4.5 Projectile Motion with Retarding Force
4.6 Numerical Solutions

4.1 More about the Horizontal motion of an object with a retarding force
In the last lecture, we talked about the motion of an object on a horizontal surface, which is affected by a velocity dependent retarding force.

We found out how the velocity and the position depend on time t.

 

------------------------- (4.1)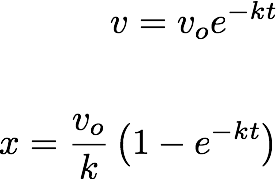  
   

Let's say we want to find the velocity as a function of time. One way to that is: to combine the above two equations as:

As shown above, you can combine the two equations and get the velocity as a function of dispacement.

We can also get this relation by the folowing approach:

The second method (Just using the chain rule) may come useful in solving other problems in the future.

Return to Top

  4.2 Effect of a Retarding Motion on a Vertical Motion

Find the displacement and velocity of a particle undergoing vertical motion in a medium having a retarding force proportional to the velocity.

Now there is no any initial velocity in the horizontal direction, neither does it have any horizontal force. The whole dynamics will be in the vertical direction.

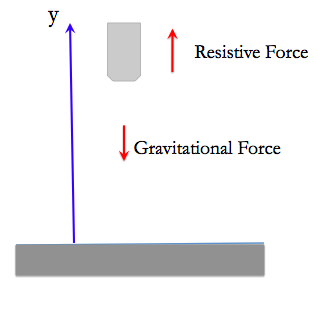
Let us consider that the particle is falling downward with an initial velocity v0, from a height h in a constant gravitational field. We consider the Newton's equation in the y direction.

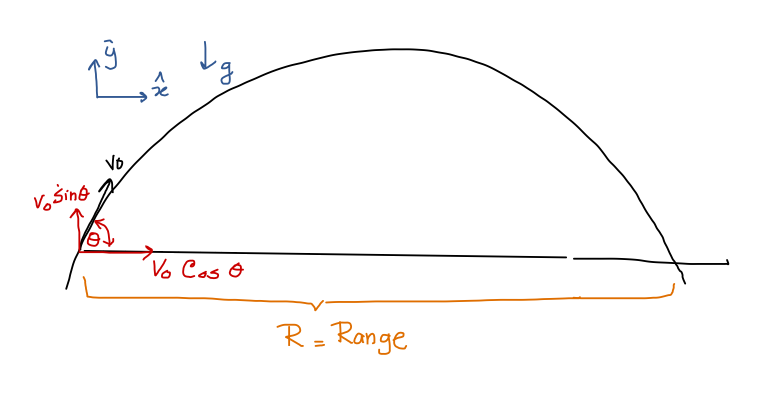
Let's pick the coordinate system as shown in the figure.

The gravitational force is in the negative z direction. As the object is moving in the negative z direction, the retarding force is in the positive z direction.

Now we have:

Now by integrating the above equation:

This gives:

By substituting the integration constant in the above equation:

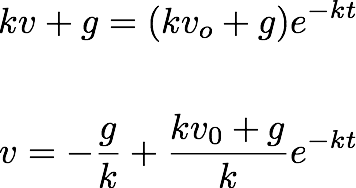
--------------------- (4.1)        

The question ans both the velocity and the position as a function of time. We found the velocity as a function of time. Now let's integrate the last equation one more time to get the position.

Using the initial conditions, (at t=0, z=h)

which gives:

4.3 Terminal Velocity

According to the equation 4.1, we see the as time becomes very long, the object gets a terminal velocity vt. (which is equal to -g/k). What does that mean?

The retarding force acting on the particle, and retarding force has become equal to the force coming due to gravity. Retarding force is a velocity dependent force and now that no force acting on the particle, there is no acceleration. Velocity doe not increase. The particle has thus come to a terminal velocity.

If you start with a velocity that is larger than the terminal velocity, the velocity decreases until you reach the terminal velocity. If you start with the zero velocity (or  a velocity less than g/k), the velocity increases to reach the terminal velocity.

Basically, what happens is, If you start with a higher velocity, Starting resistive force is large. Then the resistive force decrase the velocity of the object, resulting a decrease in the resistive force. At one point, Resistive force become equal to the Gravitational force... Thus the object is in equilibrium. Velocity will no longer change. The Retarding force will no longer change. This is therefore a TERMINAL VELOCITY

4.4 Projectile Motion with No Retarding Forces.

We have talked about the motion of an obOject in the horizontal direction, and then the motion of an object in the vertical direction. Now we are going to discuss the combination, the effect of retarding force in the Projectile Motion.

Before we do that, let me summarice some points from the Projectile Motion with no air resistance,

In previous classes, we have analyzed this problem with no air resistance. It is not hard to get the x position and y position as a function of time. (By solving the Kinematics equations or by integrating the Newton's equations)

 

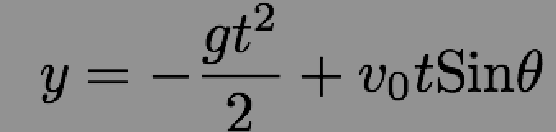
------------------- (4.2)   

We can use these two equations to find out the other knowns about the projectile motion. For example, Let's say you need to find the range of the projectile: We follow the procedure as:

We know, at t=0, y=0; The y coordinate again becomes zero at t=T, (That is where the x coordinate equals to the range R as shown in the figure). By applying the y=0 condition in equation 4.2:

That means, at time t=T, the projectile y-coordinate becomes zero. at t=T, the x-coordinate of the projectile equals to R, the range of the projectile. We can use the equation (4-2) to find R:

Notice that the maximum range occurs when the inclined angle equals 45 degrees.

Anyways, finding various unknown quantities related to the above problem is pretty straight-forward.


4.5 Projectile Motion with No Retarding Forces.

Now we are going to consider the same problem: Yet there are velocity dependant retarding forces acting on the particle. (the forces caused by air-resistance etc).

OK, Let's write the equations of motion in the same way we did earlier.

We have the initial conditions:

Through out the motion, projectile has a retarding force (which is assumed here to be proportional to the instantaneous velocity).

So the equations of motion become:

We can integrate the equation again to find the x-coordinate of the position of the projectile.

----------------- (4.3)        

(Essentially, this equals to the example 2.4 from the text)

Now By integrating the y-direction equation and using the initial conditions, we can get the y-coordinate of the position of the projectile as,

------------------- (4.4)     

Now if you want to calculate the Range in the previous problem: What you need to do is, find the time T when the projectile hits the ground (that is when y=0; by making y=0 in the equation (4-3)), and then use that time in equation (4-4) to find the x position as the projectiles hits the ground, which is named as the Range (R) of the projectile. Will that procedure work here?

OK, By applying the condition for the projectile to hit the ground (y=0) in the equation (4-4): we get the time T as:

------------------- (4.5)     

But the problem is, we cannot apply eq (4-5) in eq. (4-3) and solve for the x-position. Those are transcendental equations. We need to use an approximate mathods to find a solution.

4.6 Projectile Motion with Retarding Forces.

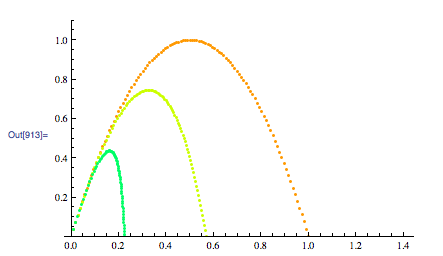
Following I show the results from  a Numerical solution to the abpve problem.

The Mathematica code is attached. (Those who check just after my class, the code will soon be uploaded)

The following Mathematica CDF player will allow you to change the parameters and look at the difference.

The above Mathematica CDF code was written by Thushari Jayasekera.

Return to Top  

PREV | 310 Home | NEXT