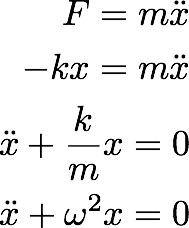DEpartment of physics

In the last lecture,We continue with the chapter 2, discussing the conservation theoroms. Conservation of Energy, Linear Momentum and the Angular Momentum. To refresh the ideas of conservation laws, we will do few problems in class. Last part of the lecture today, we will start chapter 3: on oscilliations. Different type of force that result in a periodi motion, and we will basically solve the Newtons Equations for different cases.

5.1 Work and Energy
        Examples
5.2 Oscilations

5.1 Work and Energy

In this lecture, we will be discussing about Work and energy, and reach some conservation theorems. The conservations are a consequence of Neton's Laws. We are not proving the conservation theorems. We are proving that the Newton's Laws are valid by proving the experimental validity of conservation laws in real systems.

• The total linear momentum of a particle is consrved, when there is no net force acting on it.
• When there is no torque, the total angular momentum is conserved.
• The total energy of a particle on a conservative force field is a constant in time.

The conservation laws can be used to analyze the motion. Let's start with some problems.

Example: A mouse of m jumps on the outside edge of a freely turning ceiling fan of rotational inertia I and radius R. By what ratio does the angular velocity change?

Example: A block of mass m=1.62 kg slides down a frictionless incline. The block is released at a height h=3.91 m above the bottom of the loop. What is the force of the inclined track on the block at the bottom of the incline? Refer to the Problem 2.25 in the book.

Return to Top

5.2 Oscilliations

We will be be starting the Chapter 3: Oscillations.

Why oscillations are important? Oscillatory motions can be found in many natural as well as engineered systems. Oscillatory motion is a change in a quantity that repeats in regular intervals. Examples:
                        -    Vibration of a particle attached to a string
                        -    Simple pendulum
                        -    Compression of air in a sound wave
                        -    Atomic vibration in a crystal
                        -    Orbit of a planet about a star

The object infact pass the same place in regular intervals of time. We  are looking at the oscilliation in the displacement.
There are other oscilliations which are important and useful. One example is, we can make a electrical circuit such that the charge in a capacitor change periodically in time.

We will study the properties of this oscillations as a function of time. One common thing in oscillatory systems is, they expereince resistive forces similar to those we discussed in the previous chapter. Resistive forces will not let the particle to continue motion as we discussed above. The oscillation amplitude decreases with time as a result of the resistive or damping force. The oscillation is damped, and ultimately stops the motion.

In a machine however, we want to keep the oscillation continue without damping. We can apply an external force to do that. We can apply a periodic external force or a constant external force. We will discuss how an external force effect the damped oscillatons.

So the chapter comes in three major sections:

• Simple Harmonic Oscillations
• Damped Harmonic Oscillations
• Forced Harmonic Oscillations

In the next two lectures, we will quatitatively analyze these systems using the Newton's Laws.

Simple Harmonic Osciliations:
When an object is in an equilibrium position, when you displace it away from the equilibrium (in a small displacement), the particle tries to comeback to the equilibrium position. The force which puts the particle back in the original position is called a restoring force.
The restoring force can take a complicated form. It can be a function of the displacement, instantaneous velocity etc. Here we limit our discussion for which the restoring force is a function fo the displacement: F=F(x). We can therefore expand the force function around the equilibrium position as:

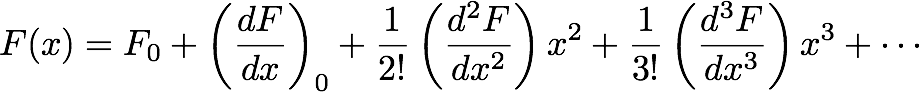
---------------------- (5.1)       

Here, F0 is the force at the equilibrium. Since it is the net force at the equilibtium,F0 must be equal to zero. Now, if we consider only the small displacements x, we can assume that all the higher powers of x are equal to zero. So the total force from eq. (5.1) can be written as:

------------------------ (5.2)        

where we have substituted,

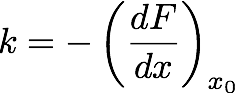
Hooke's Law:

Note that, because the restoring force F(x) is always directed towards the equilibrium position, the derivative dF/dx is negative, and the force constant k is a positive constant. This linear force behavior is called the Hooke's Law.

While in realistic problems, the restoring force can take complicated forms, the Hooke's law behavior gives a reasonable assumption for some physical problems in  nature.

Now let's solve the equation of motion of the particle with a Hook's Law type restoring force.

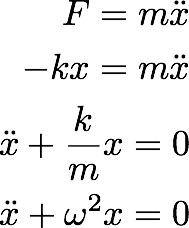
---------------- (5.3)         

This equation has the solution of the form:

----------------- (5.4)         

where the phases differ by ¶/2. This is the well-known sinusodial solution for the Simple Harmonic oscillator.

EXAMPLE: (Problem 3.7 from Text). A body of uniform cross sectional area, A=1 cm2 and of mass density \rho=0.8 g/cm3 floats in a liquid of density 1 g/cm3 and at equilibrium displaces a volume V=0.8 cm3 . Show that the period of small oscilliations about the quilibrium position is given by:

Return to Top

PREV | 310 HOME | NEXT