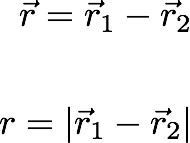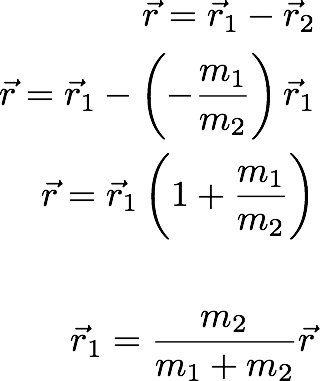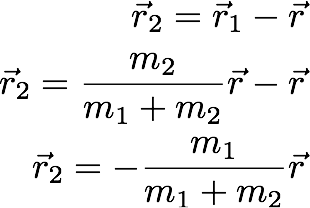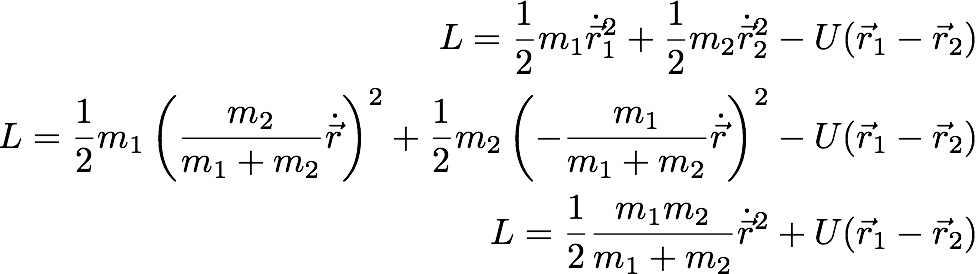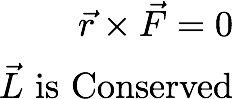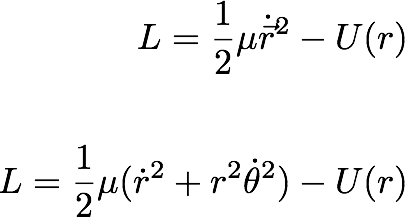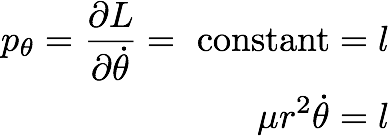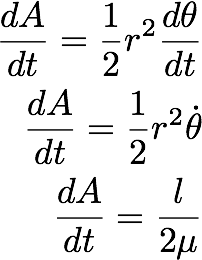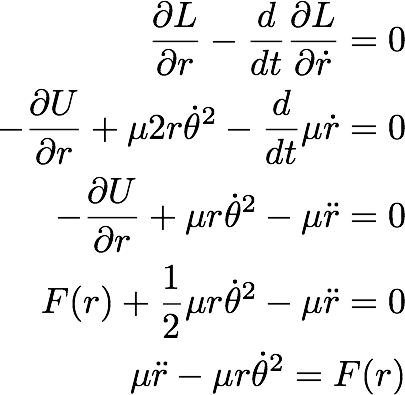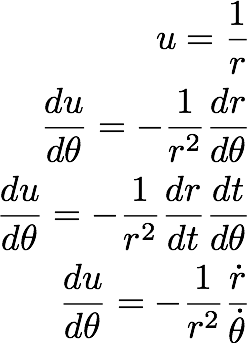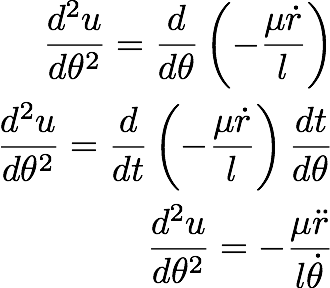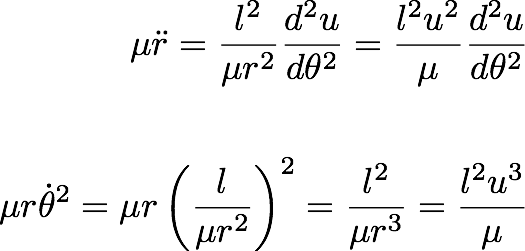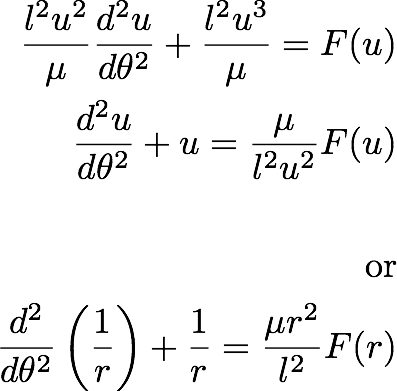Main Content Area
Lecture
31
- We are starting a new chapter today: Central Force Motion. The things we will discuss today are:
- Concept of Reduced Mass
- Conservation of Angular Momentum
- Planar Motion
- Equation of Motion for a particle Under central force field.
31.1 Central Force Motion
31.2 Motion of a Two-Body System
31.3. Angular Momentum
31.4 Euler Lagrangean Equation for Central Force Motion
31.1 Central Force Motion
What is a central force. A central force is directed along the line connecting two bodies.
Where do we see the applications of Central force?
Examples are planetary motion, Nuclear scattering etc.
So we are going to solve the equation of motion for a central force motion.
31.2 Motion of a Two-Body System
In principle, we need 6 coordinates to explain the motion of this system. We can write the Lagrangean of the system as
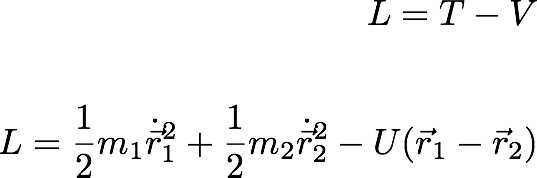
----------------- (31-1)
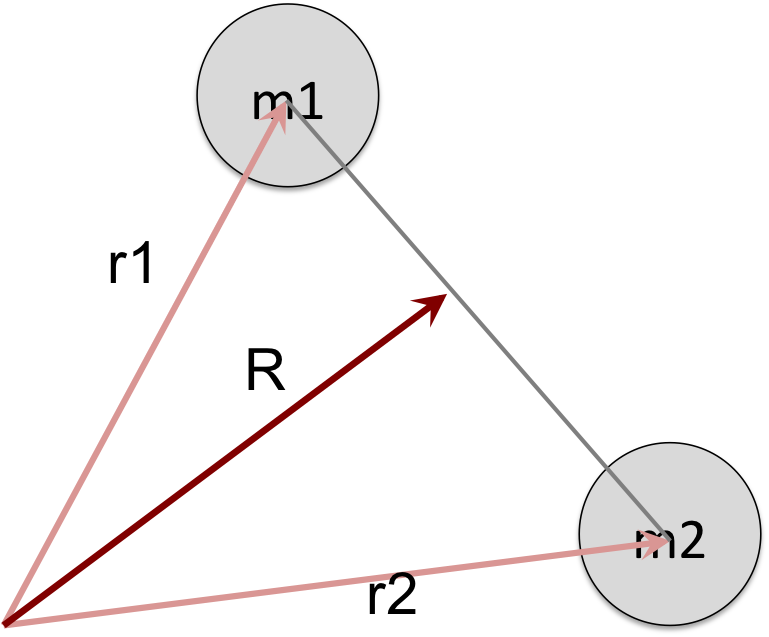
Becuase the potential energy of the system is only a function of the relative energy of the two particles. Now in the above figure, r1 is the position of the m1, r2 gives the position of m2, and R defines the center of mass for the whole system.
The center of mass is defined as:
--------------------- (31-2)
Now, if we choose the origin of the position equals to the Center of Mass of the system. That means R=0. By the vector R, we can study the translational motion of the system. But we are more interested in the relative motion. By picking the center of mass of the system as the origin of the coordinate system:
With that, the equation 31.2 becomes:
And also difine the relative coordinate as:
By combining the above two equations:
That is the angular momentum of a particle moving in a central force field is a conserved quantity.
---------------- (31.3)
Now we can also write the position of the m2 in terms of r:
This can be written as:
--------------- (31.4)
OK, Now, let;s plug this in to the eq.(31.1):
------------------ (31.5)
where we have defined the reduced mass µ.
Now the Lagrangean is a function of only one coordinate. Becasue, we have the information of the relative motion and we do not have the information on the translational motion.
31.3. Angular Momentum
Let's think about the angular momentum of the system. We know the rate of change of angular momentum can be obtained by:
Now, when we consider a central force,
What does that mean?
The angular momentum vector us conserved. The angular momentum is perpendicular to the vector r. That tells, the postion vector and momentum vector should stay in a plane, which is perpendicular to the angular momentum vector.
So we really have a two-dimensional probelm. The motion of the two-body system can be explained by a plane-polar coordinates.
So we can use the plane-polar coordiantes to explain this system. Now we can write the Lagrangean in eq. (31.5) using the plane polar coordinates.
---------------- (31.6)
Now, we can consider the Euler Lagrangean equation with respect to angle theta.
This gives
----------------- (31.7)
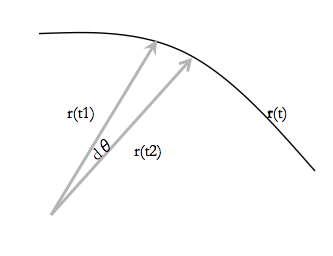
Let's represent the equation 31.7 geometrically. The figure shows the variaion of the vector r as a function of t.We can look at the coordinate system as shown in the figure.
The area covered by the vector r can be written as :
From that, we can calculate the areal velocity
That says, the areal velocity is a constant over time. This is the Kepler's Law of Planetary motion, which was obtained by experimental observations. The constant areal velocity is true for any central force problem.
31.4 Euler Lagrangean Equation for Central Force Motion
Let's apply the Euler-Lagrangean Equation as:
---------------- (31.8)
Let's change the variables:
-------------- (31.9)
By substituting from the angular momentum conservation:
gives,
Now, let;s go back to the equation of motion (eq. 31.8)
----------------- (31.10)
Next, let's write,
------------------ (31.11)
Again by substituting from the Angular Momentum Conservation:
----------------- (31.12)
Also, we have proved above that,
PREVIOUS
310HOME
NEXT