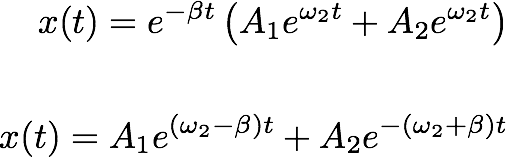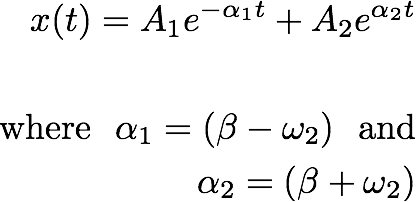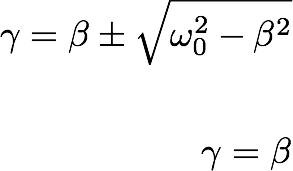DEpartment of physics

In this lecture,We we will discuss in detail about the properties of the critically damped and overdamped harmonic oscillator problem. We will also discuss one problem (The problem is not included in the website, you will get it in the class)

8.1 Damped Harmonic Oscillator (Underdamped State)
8.2 Overdamped Motion

Interactive Simulation

8.3 Critically Damped Motion

8.1 Damped Harmonic Oscillator (Underdamped State)

In the last lecture, we looked at the underdamped oscillations. We looked at how the velocity, and the position change with time.  And also we talked about the envelope function, which describes the amplitude of the vibration as a function of time.

With the Damping force, the motion does not really describe an oscilliatary motion. However, we define a damping oscillatory frequancy as:

   

Damping frequency is always less than the natural frequency of the system. Smaller the damping coefficient, the damping frequancy becomes closer to the natural frequency.

We stress the fact that the damping ocscillator is not really a periodic motion, even though the object passes throuch the origin in regualr intervals of time.

This fact is clear, if we look at the state of the object in the phase space diagram for the undamped as well as for the damped condition.

In the undamped motion, the phase space diagram is elliptical (Just make damping coefficient really small in the CDF simulation in the Lecture 7, and see,how the phase space diagram change).  In fact, the state of the object repeats in the same paths for ever.

On the other hand, the phase space for an underdamped motion deviates from theelliptical path. Observe this change in the CDF simulation. When there is a damping force, the state of the object never passes the same state. The state of the phase space keeps changing until the object comes to a rest. ( That means the motion of the object is not periodic. )

RETURN TO TOP

8.2 Overdamped Motion

We go back to the eq. (7.4) which describes the position of the object:

We can use

We can write the position coordinate as:

In the above equation, both the exponentials are negative. We can write this as:

------------------ (8.1)      

So, we solved the second order differential equation,and we get an equation as shown above with two unknowns A1 and A2. Note that Both exponents are known, becuase the natural frequency and the damping coefficients are known.

According to the eq. (8.1), x(t) is defined by two exonentially decaying functions. With these overdamped conditions, if you displace the object from its equilibroum position,the only way it comes back to the original equilibrium position is, if you wait an infinitely long time.

You can see this in the following CDF player.

The above Mathematica CDF player was created by Thushari Jayasekera

RETURN TO TOP

8.3 Critically Damped Motion

The third case we study under the damped harmonic oscillator is the critically damped motion where,

Let's recall: When we started solving this equation, we originally assumed of a solution: , substitute in the equation of motions and solve for gamma. We ended up with a quadratic equation for gamma,that gamma has two possible solutions. At the critically damped condtion however, we have only one solution for gamma as shown follows:

That means the solution for the system take the form:

------------------- (8.2)     

We started with a second order differential equation, and now we find a solution of the form (eq. 8.2), with a single unknown. We are missing something here...

Let's go back to the original equation.

---------------- (8.3)       

We have proved that      is a solution to this problem. In your Homework, you will also prove that is also a solution for the equation (8.3).

So now we can write the general solution for the critically damped condition as:

  

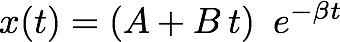
-----------------(8.4)         

Let's look at this solution. If we give an displacement to the object when there's a restoring force and the ritically damped force, the object will come back to the original position faster than the overdamped condition. In the overdamped condition, you have to wait infinitely long time for the system to come back to original. Here x(t) becomes zero if t=-A/B. (It depends on the initial conditions then.

It is clear that both in the critically damped and overdamped conditions, absolutely there are no oscillations.

Let's discuss some problems in the class.(Problems will be distributed only in the class.