Chapter 7 - Quantum Error Correcting Codes
Contents
Introduction
If information was stored redundantly in some set of quantum states, it would be possible to use the redundancy to detect and correct errors. Quantum error correcting codes aim to encode quantum information into states in just such a redundant fashion. It is worth noting that classical error correcting codes and coding theory has been around a long time and many of the ideas and methods of quantum error correction are imported from classical error correction. However, quantum error correction requires extra care when measuring to detect and correct errors because superpositions of states must be preserved. In addition, qubits can experience errors that classical bits cannot. (For example, there is no phase-flip error on a classical bit.) This chapter contains an introduction to quantum error correction including simple examples of quantum error correcting codes.
Bit-flip Errors: A Classical Code
Let us first consider a simple example of a classical error correcting code. Consider a signal which is comprised only of zeroes and ones. (For most of these notes, these are the only types of signals: bits and their quantum analogue, qubits.) An error in a sequence of zeroes and ones would occur if the sender sends a 1 and the receiver receives a 0 for one element of the sequence, or the sender sends a 0 and the receiver receives a 1. In other words, for this type of encoding, an error would be a "classical bit-flip error" which would turn a 0 into a 1 and a 1 into a 0. A simple example of a classical error correcting code which protects against such bit-flip errors is the following code. Rather than use the state 0, the state is encoded redundantly: the state 000 is used. This is called an encoded zero state or a logical zero state. Likewise, 111 is used as an encoded 1, or logical 1. Now suppose one bit is flipped when the encoded state 111 is sent, and further suppose that it is the first bit which is flipped. If one (and only one) of the bits is flipped, the encoded state could be fixed by flipping the outlier so that it agrees with the others.
Let us assume that each error is independent and has probability . The probability that the bit is not flipped is then . Since the probability is that one bit flip occurs, then the probability that two are flipped is assuming that which are flipped is unknown. The probability that three are flipped is . So the code will help us if which happens when .
This example will be used below to find a simple bit-flip code for a quantum system.
Further Reading
Appendix F contains a brief introduction to classical error correction. Many of the concepts and definitions in that appendix will be helpful for understanding the material in this chapter. However, the chapter itself is somewhat self-contained. When more explanation is required or desired, it will likely be helpful to read or reread Appendix F and/or consult the references there.
Shor's Nine-Qubit Quantum Error Correcting Code
Shor's nine-qubit quantum error correcting code is important for several reasons. Historically, it is important because it provides the first example of a quantum error correcting code which, in principle, can correct arbitrary single-qubit errors. Pedagogically, it is important because it is an example which can be understood in terms of the simple classical error correcting code given above. It also uses many of the standard assumptions of more general quantum error correcting codes. Therefore, it is presented as our first quantum error correcting code and, as will be seen later, an example of what is called a stabilizer code, which is a very general category.
The Shor code is introduced in parts, bit-flip and phase-flip, and then in its entirety. Since the phase-flip code follows from the bit-flip code (as discussed below), the bit-flip code is discussed in great detail.
Bit-flip Errors: A Quantum Code
The quantum bit-flip code uses three quantum states to encode one as does the classical bit-flip code above. The state is the logical state representing the zero state of the encoded qubit. (The subscript L is to indicate that it is a logical state and the b indicates that it is a bit-flip code. We will see below why this distinction is helpful.) Similarly, is used for the logical one state.
Encoding the Logical State
Note that one cannot just clone a state to produce redundancy due to the No-Cloning Theorem. Also, the encoded state needs to preserve superpositions such as
| (7.1) |
To encode the state redundantly, cloning is not required. The encoding can be accomplished using the gate twice. Simply apply and to the following state of three qubits,
This will produce
| (7.2) |
The circuit diagram for this is given in Figure 7.1.
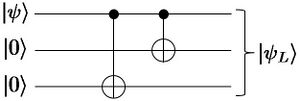
|
Figure 7.1: Circuit diagram for encoding a qubit into a 3-qubit bit-flip protected code.
Error Syndrome Extraction
Now a method for measurement and recovery is needed. The problem is that in quantum mechanics one cannot just measure the three states to see if they agree; a quantum state can be in a superposition of the (logical) zero state and the (logical) one state as above, and a measurement of the first qubit to see if it is in the state zero or not will immediately produce the state with probability and with probability , thus destroying the superposition of the qubit state. The state would then contain only classical information. (Essentially it is equivalent to the classical 000 or 111 binary state.) Since we need to preserve arbitrary superpositions, we cannot use this method for determining whether or not an error occurred.
Now let us suppose that a bit-flip error occurs on . The objective is to determine if the state has experienced a bit-flip error or not without ruining the superposition and, if it has an error, to determine which qubit experienced the error. This can be done by checking to see if the first two qubits are the same or not and then checking to see if the last two qubits are the same or not without ever determining whether the state is the logical zero, logical one, or a superposition of the two.
Let us examine this process in detail. First, notice the state is an eigenvector of with eigenvalue 1 and is an eigenvector of with eigenvalue -1. Then any logical state is an eigenstate of the operator with eigenvalue of 1 if the first two qubits are the same and -1 if they differ. For example,
| (7.3) |
Of course the same is also true for the operator . However, suppose that a bit-flip error occurs on the first qubit, giving . Then
| (7.4) |
Notice that, in principle, we need not determine either or . However, it does seem that the error can be detected. Since determining the value of the operator shows that the last two qubits agree, we know that the error occurred on the first qubit. In fact, it is not difficult to convince yourself that measuring these two operators will determine which qubit experienced a bit-flip for any of the three. Just like the classical bit-flip code, this will not indicate whether or not an error occurred on two qubits. Thus the probability must be small, just like the case for the classical code.
Now, we have the idea that we could determine the parity of the pairs of qubits to determine if they are the same or different. But how would we determine this in practice? A method for doing this is shown in Figure 7.2.
Figure 7.2: A method for extracting a bit-flip error syndrome from a 3-qubit bit-flip protected code. The M's are measurements on the ancillary qubits, the results of which are recorded as and .
Figure 7.2 gives a circuit for determining the error, also known as a syndrome measurement. In this example, a bit-flip error occurred on qubit 1 in the 3 qubit QECC. This is represented by an gate. After 4 CNOT gates, the two ancillary qubits are measured. A measurement in the basis gives a result of for the top ancillary qubit and for the bottom one. This tells us that the first qubit has had a bit-flip error. We then feed this information back into the system by implementing an gate on the first qubit, thus correcting the error.
Notice that we have not determined the coefficients of the superposition of the logical zero and logical one states. We have only determined that there was an error on the first qubit since it does not agree with the other two. (Assuming that only one bit-flip error could have occurred.)
Continuous Sets of Errors
The error, in this case represented by an gate, is not very realistic. What would be more realistic is that the bit is not flipped completely; it is in a superposition of the zero state and one state. In other words, we should properly consider the following state, where an error has occurred on the first qubit:
| (7.5) |
This is a rotation about the x-axis by an arbitrary angle with and . (See Section C.5.1.) Now suppose that two ancillary qubits are attached to the state
| (7.6) |
and the resulting state is put into the circuit that gives the error syndrome given in Figure 7.2. Let . Then
| (7.7) |
,
where the two ancillary qubits, denoted (for the first ancillary qubit which is on top in Figure 7.2) and (for the second ancillary qubit which is on bottom in Figure 7.2), will give the error syndrome. The measurement of the second ancillary qubit always gives . The measurement of the first gives with probability and, if this occurs, the system will be in its original state and there is no error. However, if the measurement of the first ancillary qubit gives , which it will with probability then the system is left in the state
| (7.8) |
This indicates that a bit-flip error has occurred on the first qubit. Such an error is easily corrected with an gate on the first qubit, which will flip it.
Therefore any single-qubit bit-flip error can be corrected, since we will project into the basis of one bit-flip error and the syndrome measurement indicates which one. In other words, we have made the error discrete using a projective measurement of the ancilla.
Phase-flip Errors
"Phase-flip errors" are errors which change the sign of the state. This is not a classical error as it does not occur on a classical bit. However, it does occur on qubits that are not in the zero state. Thus these errors must be treated.
Much of what works for the bit-flip errors also works for phase-flip errors once we are able to encode properly. Let us consider the following states that we will used to encode our logical qubit:
| (7.9) |
In this case, when a "phase-flip" occurs, the becomes a or vice versa. Therefore it is similar to the bit-flip error since there are two orthogonal states that are changed into one another by the error. In this case the error operator is of the form . As before, if a phase error occurs on the first qubit, then we can encode redundantly by letting and . It is easy to see that this code will enable the detection and correction of one phase error just as the bit-flip code did for one bit-flip. In this case we exchange the in the bit-flip code with a for the phase-flip code and the process carries through as before.
Bit-flip and Phase-flip Errors
Certainly if a phase-flip error does not have a classical analogue then the combination of bit- and phase-flip errors also does not. It turns out that by having found a code that will protect against bit-flip errors and another against phase-flip errors, we are able to write down a code that will protect against both. This was first given by Peter Shor Shor:1995 [17], but was also described by Carlton Caves in a very readable paper, Caves:1999 [18].
The way to protect against both is to combine the two codes and take the logical qubits to be
| (7.10) |
One may also write this as
| (7.11) |
This shows that there is a code which protects against bit-flip errors and phase-flip errors by using a redundant encoding comprised of the states that protect against bit flips and the states that protect against phase flips.
Quantum Error Correcting Codes: General Properties
Now that we have seen some examples of quantum error correcting codes, some natural questions come to mind. Are there general rules for constructing quantum error correcting codes? In the case of classical codes, there is a disjointness condition and a Hamming bound. These let us know when it is not possible to construct a quantum error correcting code. Here, the two analogues for quantum error correcting codes are given, although the disjointness condition is quite different for quantum error correcting codes.
The Quantum Error Correcting Code Condition
Let us consider a quantum system undergoing some noisy evolution. As described in Section 6.2 and Section 6.3, such an open-system evolution can be described by a quantum operation acting on a density operator,
| (7.12) |
The operator elements can be used to express what is known as the quantum error correcting code condition (See Nielsen and Chuang [2], or Nielsen, et al:97 [29] for the original reference),
| (7.13) |
where the are the operators from the operator-sum representation, and is a projector onto the code space. An equivalent expression is (see Knill and Laflamme),
| (7.14) |
This is the quantum analogue of the disjointness condition for classical error correcting codes. To interpret this, consider Equation (7.14). This says that if one error acts acts on a logical state and another error (or possibly the same error) acts on a different logical state , then the two cannot be equal. In fact, the statement is a bit different. It tells us that there can be no overlap between two states. If there were overlap, there would be some probability for a measurement to produce an ambiguous result. It also tells us that for two different the same error acting will produce the same result. This is allowed by the superposition principle, but not something one finds in classical error correction. Therefore, the analogy with the classical disjointness condition is very loose. (See Knill and Laflamme for further explanation.)
One way to understand Equation (7.13) is to show Equation (7.14) is true if and only if Equation (7.13) is true. However, these results can be seen as part of a broader and more basic property of quantum systems related to the reversibility of a quantum operation as discussed by Nielsen, et al:97 [29].
A Basis for Errors
Using the Pauli matrices and the identity for the errors, any error can be described as a tensor product of operators. Each term in the tensor product will involve one of four operators, , , or , where the identity indicates that no error has occurred. (See Section 6.5.) For example, suppose a code involves five qubits. For each of the five qubits, suppose no error occurs on qubit 1, a bit-flip error occurs on qubits 2 and 3, a phase error occurs on qubit 4, and qubit 5 is affected by both types of errors. This error operator would be
| (7.15) |
or, using a short-hand notation,
| (7.16) |
This error operator is said to have weight four.
Definition 1: weight of an operator
The weight of an operator is the number of non-identity elements in the tensor product.
This provides us with a basis for all errors that can occur. This is enough, since the errors can be made discrete using the syndrome measurement process.
Definition 2: Distance of a Quantum Error Correcting Code
The distance of a quantum error correcting code is the minimum weight, greater than zero, of an element of the Pauli group such that the quantum error correcting code condition fails (i.e., such that is not satisfied).
Quantum Error Correction for Errors
A quantum error correcting code that uses qubits to encode logical qubits and can correct up to errors is denoted . This is similar to the classical code notation except that double brackets are used to distinguish the quantum code from the corresponding classical code. Using , this is also written . When a code satisfies the more restrictive condition in Equ. (7.14), the code is called non-degenerate. Note that Equ. (7.14) indicates the set of errors which needs to be corrected given by the operator elements of the operator-sum representation. It turns out that one can choose the set of errors to be described by an orthogonal basis. This is done using the unitary degree of freedom in the operator-sum representation from Section 6.4. Nielsen and Chuang [2] use this to show that the conditions Equ. (7.13) are necessary and sufficient for the existence of a quantum error correcting code. Thus the necessary and sufficient conditions for being able to correct errors are given by Equ. (7.13), or equivalently, Equ. (7.14).
The Quantum Hamming Bound
Like the classical Hamming bound (Section F.4), the quantum Hamming bound is a simple bound on the size of the code for correcting a given number of errors. In other words, it provides a bound on the rate of the code, . The main difference is that there are three types of errors that can occur to a qubit: the three Pauli matrices , , and . So each error comes in three types. The number of possible error operators of weight acting on a code of qubits is , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(n,t)\;\!} is the binomial coefficient. Therefore since every logical state (and every logical state with any error acting on it) must all be mutually orthogonal, the quantum Hamming bound states that this set must be less than or equal to the total number of states in the Hilbert space, which is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^n\;\!} . That is,
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\sum_{i=0}^t 3^i C(n,i) \leq 2^n, \,\!} | (7.17) |
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\;\!} is the number of code words.
Just as in the classical case, when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m= 2^k\;\!} , we may take the logarithm of the equation along with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n,t \;\!} large to get
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k/n\leq 1-(t/n)\log 3-H(t/n), \,\!} | (7.18) |
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x) = -x\log x -(1-x)\log(1-x)\;\!} and all logarithms are base 2.
Equation (7.17) tells us that the smallest possible code encoding one qubit such that it can be protected against one arbitrary error has 5 physical qubits encoding one logical one. (Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=2 (k=1), t=1 \;\!} so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=5 \;\!} .)
Stabilizer Codes
The mathematical definition of a stabilizer is given in Section D.6.1. Loosely speaking, it is a subgroup of transformations that leave a particular point in space fixed. The theory of stabilizer codes is based on this notion.
Stabilizer codes are a family of quantum error correcting codes which are describable by using the stabilizer of a state (really a set of states) in the Hilbert space. They are distinguished for several reasons. One, they form a large class of quantum error correcting codes. Two, they are conveniently described by their operators rather than their states and show that this can generally be the case for many quantum error correcting codes. Other reasons will be discussed later.
Introduction
We will begin by revisiting the three-qubit quantum error correcting code presented in some detail in Section 7.2.1. Recall that a bit-flip error that has occurred on one of the three qubits used in the logical qubit would be detectable if we could measure the parity of pairs of qubits. These operators could be chosen to be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_1Z_2\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_2Z_3\,\!} , although any two non-identical pair would work. Note that the basis states Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |000\rangle\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |111\rangle\,\!} , as well as any linear combination of these states, are eigenstates of these operators with eigenvalue +1. The states with a single correctable error are eigenstates of these operators, but one will have eigenvalue -1. The operators that give one of the single qubit bit-flip errors are either Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_1\,\!} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_2\,\!} , or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_3\,\!} . This is the idea behind stabilizer quantum error correcting codes. The stabilizers act as parity checks on the code words.
The stabilizer is a subgroup Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{S}\,\!} of the Pauli group, which is an abelian subgroup (this means all elements commute with each other). However, the elements Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_1\,\!} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_2\,\!} , or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_3\,\!} anti-commute with at least one element of the stabilizer. So the parity check describable by saying that states with errors are eigenstates of the stabilizers with eigenvalue -1 is equivalent to saying that one of the stabilizer operators will anti-commute with an error operator.
The elements of the stabilizer stabilize code words, that is, code words are eigenstates of the stabilizer operators with eigenvalue +1, and states with errors have eigenvalue -1 and this can always be chosen to be true for this class of quantum error correcting codes. Note that if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle\,\!} is a code word, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\in \mathcal{S}\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\,\!} is an error operator, then
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} SE|\psi\rangle &= S|\psi^\prime\rangle =(-1)|\psi^\prime\rangle \\ ES|\psi\rangle &= E|\psi\rangle = |\psi^\prime\rangle. \end{align}\,\!} | (7.19) |
or
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)SE|\psi\rangle = ES|\psi\rangle. \,\!} | (7.20) |
This says that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SE + ES =0\,\!} when acting on the code words. In other words, the operators anti-commute when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\,\!} produces a state that has eigenvalues -1 and also when it is a state that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\,\!} stabilizes. Errors anticommute with some element of the set of stabilizer elements.
This is the basic idea of the stabilizer code construction to be discussed in general in the next section.
General Stabilizer Formalism
This brief section provides general definitions and theorems for stabilizer quantum error correcting codes. The next section provides an explicit example.
Definition 3: Stabilizer Code
Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{S}\subset \mathcal{P}_n \,\!} be an abelian subgroup of the Pauli group that does not contain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I},\pm i\mathbb{I}\,\!} . Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}(\mathcal{S}) = \{|\psi\rangle \; |\; S|\psi\rangle=|\psi\rangle, \mbox{ for all } S\in \mathcal{S}.\,\!} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}(\mathcal{S})\,\!} is a stabilizer code and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{S}\,\!} is its stabilizer.
This formalizes what was stated earlier, which is that all states of the code space are eigenstates of elements of the stabilizer subgroup with eigenvalue +1. However, it also says more. It tells us that any subgroup of the Pauli group that is abelian and does not contain the elements Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I},\pm i\mathbb{I}\,\!} can be used to construct a stabilizer code by simply choosing the set of states that are eigenstates with eigenvalues +1. Another way of saying this is that the states are fixed, or invariant, under the action of the stabilizer elements. Let us see why the restriction not allowing Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I},\pm i\mathbb{I}\,\!} must be included. Suppose that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I}\,\!} was in the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{S}.\,\!} It then follows that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I}|\psi\rangle = |\psi\rangle\,\!} . Only the zero state satisfies this equation, so the code must contain no states other than the zero one. (The states must be +1 eigenstates of every stabilizer element.) Now, suppose one of the other two was in the stabilizer subgroup. This means that the element squared is also in the stabilizer, since it is a subgroup and must be closed under multiplication. But the square of these gives Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbb{I}\,\!} , which cannot be in the set. Thus none of these can be included.
Encoding/Decoding from Stabilizer Generators
Once one has obtained the stabilizer subgroup, it is left to find the codewords that are states with eigenvalue +1. To do this, one only needs to ensure the generators of the stabilizer satisfy this condition, since the generators give all other stabilizer elements through multiplication. Therefore, if the state has eigenvalue +1 for all generators, it will also have eigenvalue +1 for all stabilizer elements.
For smaller codes, finding the set of states could be as easy as satisfying constraints given by the small number of generators. Larger, more complicated codes may however require a lot of work to find the states. Cleve and Gottesman gave an algorithm for finding the code words using a efficient gate array obtained from the stabilizer formalism. http://arxiv.org/abs/quant-ph/9607030
It is worth noting that the decoding and error detection and correction steps also require work to find explicit circuits. However, for many stabilizer codes, decoding is simply encoding in reverse. (This is not so for every quantum error correcting code.)
Although these accomplishments are very important, more work is required to ensure circuits are fault-tolerant---that errors do not propagate or grow as the computation progresses. If they were to develop without these constraints, then the computation would eventually fail.
A Return to Shor's Code
Let us consider the set of operators in Table 7.1 where each operator in the row is included, in order, in the tensor product that forms an element of the Pauli group. These elements form the eight generators of stabilizer elements Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i\,\!} . The order of the stabilizer subgroup is much larger than the set of generators, which is only 8. Here they are taken as in the table, but the set is not unique. This set is chosen to agree with our earlier choice of measurements.
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i\in \mathcal{S}\,\!} | q 1 | q 2 | q 3 | q 4 | q 5 | q 6 | q 7 | q 8 | q 9 |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_1\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_2\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_3\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_4\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_5\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_6\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_7\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_8\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} |
Having the generators of the stabilizer of the code, the objective is to construct the codewords, or the explicit states that are eigenstates of these operators with eigenvalues +1. From the top row, it is clear that the first two qubits must be the same, whether zero or one, so that the parity is even. Similarly, the second two must be the same, and thus the first three must be the same. Similarly, the middle three and last three must also be the same. The last two generators state that flipping the first six bits at once will produce the same state, and flipping the last six bits together will produce the same state. Thinking of these in blocks (since the first six generators give blocks of three) tells us that there are states that are symmetric under the interchange of zeroes and ones in pairs of triplet blocks. To break this into two parts, one may choose the symmetric and anti-symmetric combination of states that leads to the Shor code words given in Equation (7.10).
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\!}
CSS codes
There is a class of quantum error correcting codes called the CSS codes after their inventors Calderbank and Shor [31], and Steane [32]. These are also stabilizer codes, but their construction is different and somewhat informative due to the connection to classical error correction. However, given that they are stabilizer codes, the stabilizer formalism and tools can be used for encoding, etc.
The CSS codes are constructed from two classical linear codes, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_1\,\!} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_2\,\!} . This is done by taking advantage of the parity check matrices from the classical coding theory. In this section, this construction is briefly described. In the next section, the seven qubit CSS code is described.
Recall from the discussion of the Shor code that a phase-flip code can be constructed from a bit-flip code by using Hadamard gates in order to change the basis from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle,|1\rangle\,\!} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |+\rangle,|-\rangle\,\!} . Thus all of the error detection and correction can be accomplished by translating from one basis to the other.
Keeping this in mind, a quantum error correcting code can be constructed from a classical error correcting code using the following trick. (See Steane [32] or the review by Gottesman [30].) Take the classical parity check matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1\,\!} for a classical error correcting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n_1,k_1,d_1]\,\!} code Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_1\,\!} , replace all zero entries with the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I} \,\!} operator (matrix), and replace all one entries with the Pauli matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \,\!} . This will turn the rows into a set of stabilizer elements that will detect and correct Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_1=(d_1-1)/2\,\!} bit-flip errors, just as did the classical code. Then, given another classical error correcting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n_2,k_2,d_2]\,\!} code Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_2\,\!} , replace all zero entries with the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I} \,\!} operator (matrix), and replace all one entries with the Pauli matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X \,\!} . This will give turn the rows into a set of stabilizer elements that will detect and correct Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_2=(d_2-1)/2\,\!} phase-flip errors. This would give a stabilizer code with one possible caveat: the operators in the stabilizer all need to commute with each other. The way to ensure this will happen, that the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X \,\!} generators and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \,\!} generators commute, is to combine the codes in a particular way.
The dual of a code (denoted Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}^\perp\,\!} ) is also a code, and it is not too difficult to show that the parity check matrix for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}\,\!} is the generator matrix for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}^\perp\,\!} . It turns out that if (and only if) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_2^\perp \subseteq \mathcal{C}_1\,\!} , then the two codes combine to produce an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [[n,k_1+k_2-n,d]]\,\!} stabilizer code, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\geq \text{min}(d_1,d_2)\,\!} . That is, the generators for each of the two codes will commute with each other.
Now the two codes, one to protect against bit-flips and one to protect against phase-flips, combine so that they can correct any error, including Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y\,\!} errors that are composed of both a bit-flip and phase-flip. Therefore the code can protect against both, and the minimum distance is the smaller of the distance of the two codes. It could actually be higher if the code is degenerate.
Steane's Seven Qubit Code
The seven qubit quantum error correcting code, originally described by Steane, is member of the class of CSS quantum error correcting codes. In fact it is the smallest such code, and has Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_2 = \mathcal{C}_1\,\!} . It is a quantum error correcting code, using 7 qubits to encode one logical (or data) qubit such that one arbitrary error can be detected and corrected. This code has been studied extensively, since it is able to be made fault tolerant (explained below).
This code is actually based on the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [7,4,3]\,\!} Hamming code discussed in Appendix F. Let us first recall the parity check matrix
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \left(\begin{array}{ccccccc} 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 \end{array}\right) \,\!} | (7.21) |
and the generator matrix
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = \left(\begin{array}{ccccccc} 1 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right). \,\!} | (7.22) |
Relating this back to the stabilizer formalism, the generators can be written using the parity check matrix as described above. They are given in Table 7.2. The first three rows each give the elements of the tensor product, in order, for the stabilizer elements of a code that can protect against bit flips. The next three give stabilizers for the phase-flip code. From these one may get the code words. The logical zero and one are given below.
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i\in \mathcal{S}\,\!} | q 1 | q 2 | q 3 | q 4 | q 5 | q 6 | q 7 |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_1\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_2\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_3\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_4\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_5\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_6\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}\,\!} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\,\!} |
Steane's 7-qubit code encodes the logical zero using all even weight classical code vectors,
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0_L\rangle = \frac{1}{\sqrt{8}} \sum_{\text{even }v} |v\rangle. \,\!} | (7.23) |
The odd weight classical code vectors are used to encode the logical one state,
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1_L\rangle = \frac{1}{\sqrt{8}} \sum_{\text{odd }v} |v\rangle. \,\!} | (7.24) |
Continue to Chapter 8 - Decoherence-Free/Noiseless Subsystems
or






























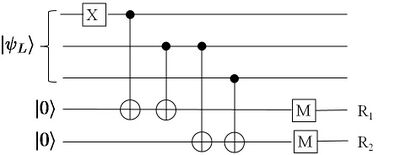














































![{\displaystyle [[n,k,2t+1]]\;\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e93c13a298688d2c49991db32bf2bc64cd71b5)

![{\displaystyle [[n,k,d]]\;\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f52efd5b3953fbb0f36e02e8423faac458aa6b8)




![{\displaystyle [[7,1,3]]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c00b70ee459440814a3dda5a2a14be2f31b1f605)