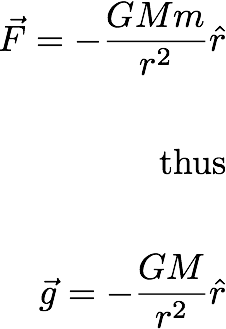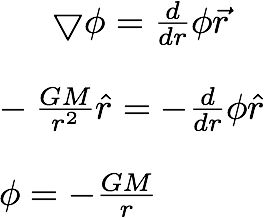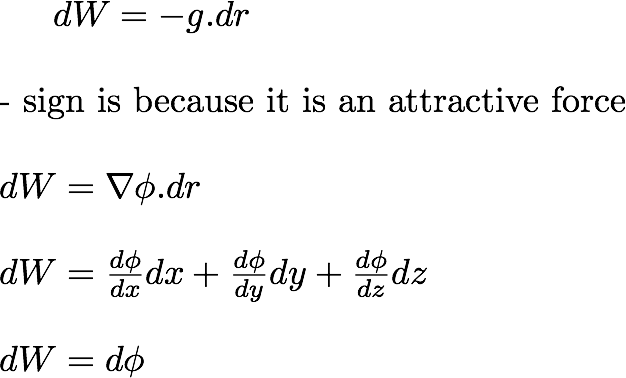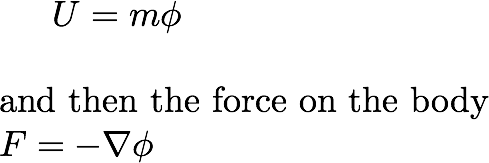DEpartment of physics

In this lecture, we will discuss the Newton's Law of gravitation, talk about how to calculate the force on a particle of mass m, due to another point-like particle. We extend this to find out the gravitational force due to a distibution of mass.  When we calculate the gravitational force due to an elemental mass and sum it (integrate or direct sum) to get the total force, we have to do a vector sum, which is not really easy. Alternate methods are useful. We define thegravitational Field vector, g, and figure that, it can be written as a gradient of a scalar quantity, which is called the gravitational potential. In this lecture, we discuss how to use gravitational potential to calculate the force due to a mass distribution.

12.1 Newton's Law of Gravitation
12.2 Gravitational force due to a Point Mass
12.3 Gravitational Force due to a distribution of mass
12.4 Gravitational Field Vector
12. 5 Gravitational Potential
            Physical Meaning of Gravitational Potential
12.6 Example: Gravitational Potential due to a Spherical-Shell type Mass



12.1 Newton's Law of Gravitation
OK.... We have discussed how to apply the Newton's laws to understand the motion of particles under the forces, such as gravitational forces, resistive forces, restoring forces, external applied forces etc.,  which are very straight forward.

Now in this lecture, we will move on to the next chapter: Gravitation.

Gravitation goes back to the story of Newton and apples.

Where should we start. Each mass particle attracts any other mass particle. It can be any type of mass. It can be people. It can be planets and us, planets with other planets, planets with the sun... etc. Gravitaonal forces are every where.

In this chapter, we basically look at the forces between us and the earth.

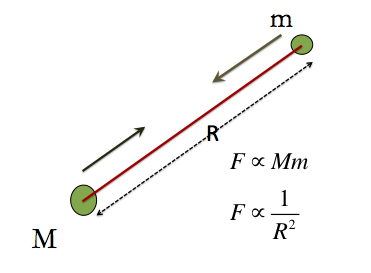
In general: Newton's law states that each mass particle  attracts each other particles in the universe with a force, that varies directly as the product of the two masses, and inversely as the square of the distance between them.

----------------- (12.1)        

RETURN TO TOP

12.2 Gravitational Force due to a Point Mass

The Newton's law was experimentally verified and the value of the Gravitational constant G was experimentally obtained. (in 1798).

The proportionallity constant G is the Gravitational Constant.

Notice that

• Gravitational force is always attractive
• Gravitational force is extremely small.... What Does that mean? If you think about two particles, both of 1kg each and 1 m apart

            So by putting it in the above equation (12.1) with G=6.67 x 10^{-11} Nm^2/kg^2,

we can get the force between the particle equals to F=1x10^{-11} N

That is an extremely small force.

That is why we say gravitational force is a small focre.

Also the attraction force on you  really depends on where you are relative to the second body your are considering. Let's think about the force on you due to the Earth. That is the gravitational force on you due to the earth.

g is the well-known gravitational accelleration constant.

RETURN TO TOP

12.3 Gravitational Force due to a Distribution of Mass

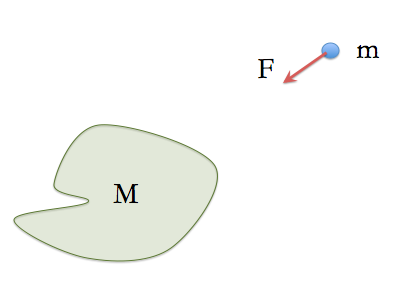
In taking the force on the particle m, we have assumed that both particles are point-like particles. which is not the case always. Let's for example think about the following situation. The gravitational attraction on mass m (which is a point like mass) due to a mass distriubtion as shown below.

How do we do it? We already know how to find the force on m due to a point mass in M. If we consider the mass M as a collection of small point masses, we can find the force component due to each point mass, and then collect all the force to find out the total force due to the mass M.

In other words, It is possible to calculate the total net gravitational force on a particle due to many other particles by simpy taking the vector sum of individual forces.

Let's consiider a mass element  at the position defined by the vector r' from the origin, as shown in the figure.

The gravitational force between the mass m and the mass element  can be writeen as follows.

Now in order to get  the force on m due to the total mass M, we will have to sum up all the from all mass elements.

If we consider a escrete system, the total force is the sum of all the forces due to mass elements.

Since in this case, we have a continuous mass distribution, the sum converts to an integration.

If both masses m and M are not point particles, we will have a double integral here. Notice that here we are doing a vector sum. In principle, given the sahpe of the two bodies, we can perform the abpve two integrations, we can evaluate the integrals.

We will do some problems to understad this. But before we move on to the problems, let's discuss about another important quantitty: Gravitational Potential.

12.4 Gravitational FIeld Vector

Let's think about the gravitational field vector.

If we think it in trms point masses,

RETURN TO TOP

12.5 Gravitational Potential

Notice that, gravitatioal field has an electrical analog. F=qE, the Force per unit electric charge is the Electric Field E.

Here, in the gravitational field, F=mg, the gravitational force per unit mass is the gravitational field, F.

Electric field inversely proportional to the square of the distance between two charges.

Gravitational field also is proportional to the square of the distance between two masses.

Both these force fields vary as 1/r^2. That allows us to write the force field in terms of a gradiaent of a scalar function.

We can identify the quantity, gravitational potential as the energy per unit mass. Since g only depends on r, as we showed earlier, we can write gradient as

---------------(12.2)       

Notice that we did not add the constant of integration, That means, when we calculate the potential from the above equation (12.2), we are off by a additiveconstant.

That means, the absolute potential energy does not have a much of a meaning. The difference in two potential energies do have meaning.

In order to fix this, we define that the potential energy goes to zero as r goes to infinity.

Now again by going back to what we have been discussing,  we can find the potential due to a volume mass can be calculated by considering the potential due to a volume element and then by integrating over the whole space:

In the similar way, we can also calculate the potential energy due to a surface mass, or the potentail due to a line mass.

Remember in the previous case, when we were looking at the force due to a mass element and summing them up to get the effect from a mass distribution, we have to consder a vector summation becuase Force is a vector.

Now, that the potential is an scaler, it is easier to do the summation and then perform the gradient of the potential to find the force.

RETURN TO TOP

Physical Meaning of the Vector Potential:

g is the gravitational field vector, or the force of an object of unit mass in the grvitational field.
Now, let's say, the object of the unit mass displace distance dr in the force field. What is the work done, inorder to move the object.

That is: the change in potential between two points is equa to the amunt of work that must be done on a body of unit mass to move it from one position to another position, in the gravitational force field.

If we define the otential to be zero at infinity, the gravitational potential at any point can be defined as the work per unit ass required to bring the body from infinity to that point.

The if U is the potential energy,



That means, if we can calculate the potential U, we can calculate the forces.

12.6 EXAMPLES:

Let's calculate the potential energy in space due to different types of mass distributions.

Gravitational Potential due to a Spherical Shell:

Find the PDF here