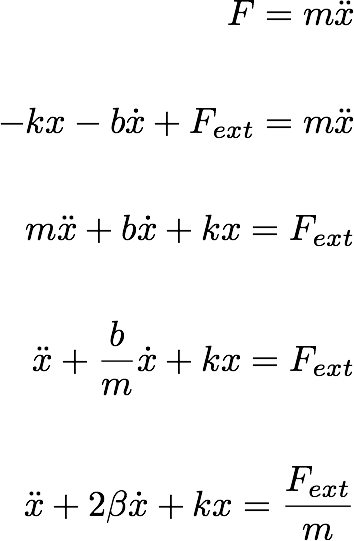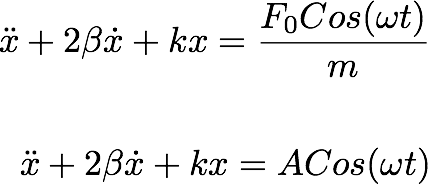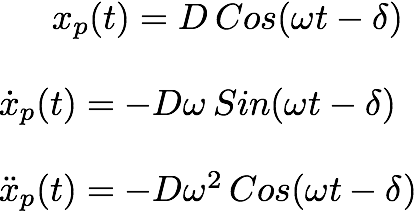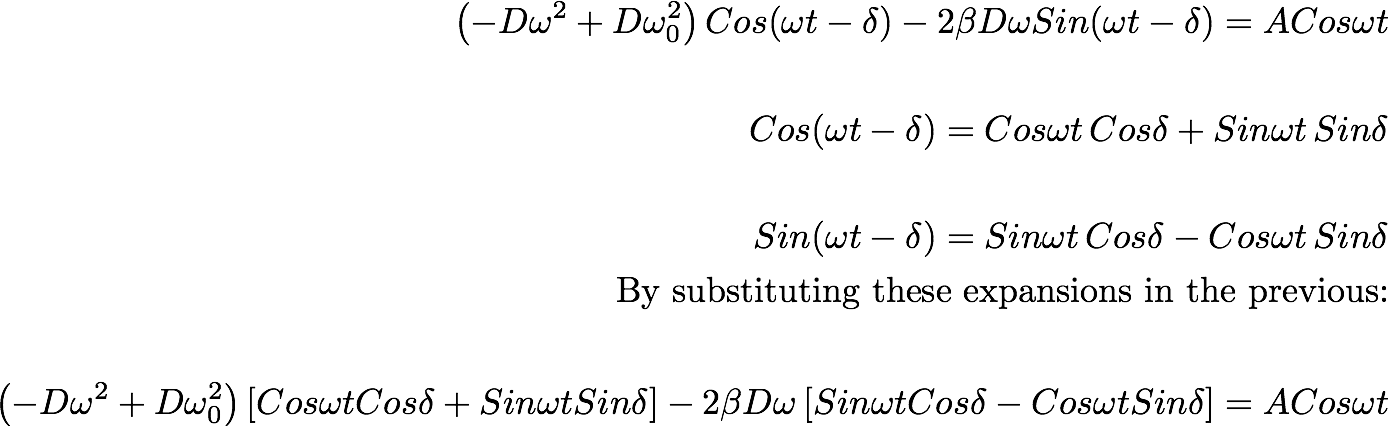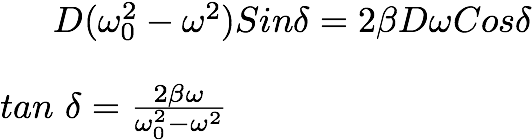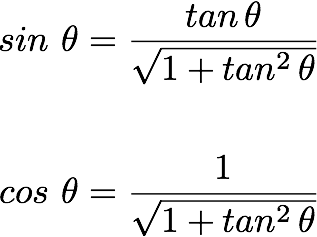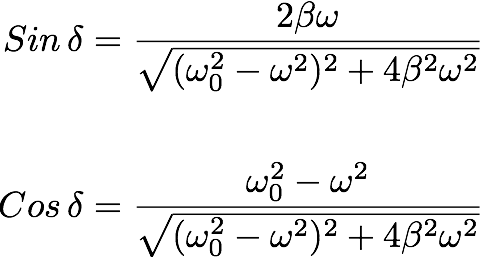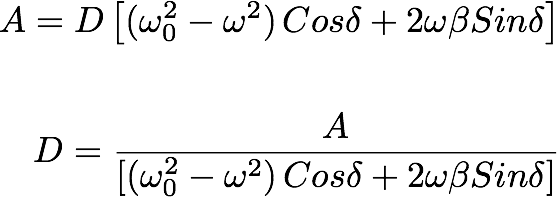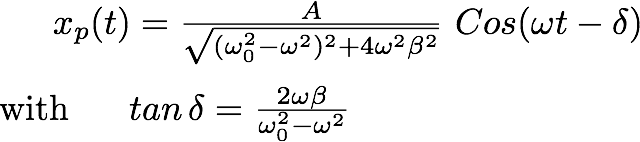DEpartment of physics

In this lecture,we will discuss the effect of driving forces on the damped harmonic oscillator. We talk about the general solution to this problem, and graphicall visualize it.

9.1 Driven Harmonic Oscillator
9.2 Complimentary Solution
9.3 Particular Solution
9.4 Interactive Graphical Representation

9.1 Driven Harmonic Oscillator

In the previous lecture, we discussed how the amplitude of the SHO decreases as a result of a resistive force. There are three cases, underdamped, criticaly damped and overdamped. As these names state, these conditions are categorized by how large the damping forces are (compared to restoring forces). In  the case of overdamped and critically damped motions, absolutely no oscillations are possible.

In the case of underdamped motion, the object still undergoes some oscillatory motion. ( Well.. in principle they are not really oscillatory as we showed in the phase space diagrams. ). We discuss how  the amplitude exponentially decreases as a function of time in this underdamped motion. In this lecture, we will discuss how we can drive the underdamped motion by an external force.

Let' start with the Newton's equation for this motion:

In principle, the external force can be of any form. We are going to start analyzing the problem for some special types of forces.
Let's consider a Sinusodial type external force.

--------------(9.1)
       

In order to find x(t), that satisfies the equation (9.1),let's refresh the knowledge about how to solve a inhomogeneous second order equation.
Let's say we want to solve:

-----------------(9.2)    

Let's say x(t) = u be a solution to the equation:

That means:

and let's say x(t)=v be a solution to the equation:

That means:

Then, we can prove that,  x(t)=u+v is also a solution to the equation (9.2):Given that, there are two possible solutions to the equation (9.1).

9.2 Complimentary Solution
The first solution: x=xc(t), which satisfy the equation  is known as the complimentary solution.In fact, we now know the complimentary solution which was found in the previous section.

--------------(9.3)     

RETURN TO TOP

9.3 Particular Solution

Now we have to solve for the particular solution xp(t) which satisfy the equation (9.1):

Let's try a solution of the form:

Let's substitute the above in the equation (9.1):

Note that in the above equation, there are two frequencies:

We can re-write this equation as:

--------------(9.4)      

This equation takes the form: , which requires both the coefficients P and Q to be zero.

That gives,

----------------(9.5)      

When we look carefully, this is an important quantity. Delta is infact, the phase difference between the driving force and the position coordinate. Using the equation (9.5):

Which gives:

---------------(9.6)

From the coefficients of Cosine in the equation (9.4),

Now by using eq. (9.6) and after some algebra, we get:

 

By putting everything together, we get the solution (the particular solution for the driven Harmonic oscillator with a Sinusodial driving force as:

--------------(9.7)     

We have found the complimentary and the particular solution for the driven oscillator (with natural frequency \omega_0)  for a sinusodial driving force of the form A Cos \omega t. (Equations 9.3 and 9.7)

That menas \delta gives the difference between the action of the driving force and the response of the system.

The general solution is

x(t)=xp(t)+xc(t)

9.4 Interactive Graphical Representation

We can see in the following mathematica code the position coordinate as a function of the time. You can see, depending on the time, either complimentary or the particular solution are dominant.

The above CDF simulation was created by Thushari Jayasekera

As the above Mathematica simuation visualizes, we can see that, the complimentary solution represents the decreasing amplitude of the damped oscilliator.The particular solution is what is important in the steady state. How long does it take to come to the steady states is heavily depend on how damped the system is.

If the damping constant is high, the complimentary solution dies out very fast, that the system comes to a steady state faster.

9.5 Resonance Phenomena

In the previous calculations, we found that, the amplitude f the final displacement of the object is a function of the driving frquency. It also is a function of some system properties such as natural frequency and the damping coefficient.

Now we are going to find out if there is a way that we can achieve the resonance phenomena, where the amplitude of the position coordinate becomes maximum. We basically look for the condition that gives a maximum amplidude D for the position coordinate. We will look at how D changes as a function of the frequancy of the driving force.

Let's discuss this in the next class.